
题目列表(包括答案和解析)
| x2 |
| a2 |
| y2 |
| b2 |
| b2e2 |
| a |
| x2 |
| 4 |
| y2 |
| 3 |
. |
| OP |
. |
| OA |
. |
| OB |
| 10 |
| 7 |
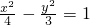 的弦,且MN与x轴垂直,A1、A2是双曲线的左、右顶点.
的弦,且MN与x轴垂直,A1、A2是双曲线的左、右顶点.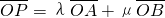 (O为坐标原点,λ,μ∈R)
(O为坐标原点,λ,μ∈R)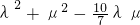 为定值,并求出这个定值.
为定值,并求出这个定值.| x2 |
| 4 |
| y2 |
| 3 |
| . |
| OP |
| . |
| OA |
| . |
| OB |
| 10 |
| 7 |
 的弦,且MN与x轴垂直,A1、A2是双曲线的左、右顶点.
的弦,且MN与x轴垂直,A1、A2是双曲线的左、右顶点. (O为坐标原点,λ,μ∈R)
(O为坐标原点,λ,μ∈R) 为定值,并求出这个定值.
为定值,并求出这个定值.一.选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
B
B
C
A
C
B
A
二.填空题
11.  12. ② 13.
12. ② 13.  14.
120 15.
14.
120 15. 
三.解答题
16.解:(Ⅰ) . …………………………………3分
. …………………………………3分
由 ,得
,得 .
………………………………5分
.
………………………………5分
(Ⅱ)由(Ⅰ)得 . ………………8分
. ………………8分
由 ,得
,得 .
.
 当
当 ,即
,即 时,函数
时,函数 有最大值
有最大值 . ……………………12分
. ……………………12分
17.解:设此工人一个季度里所得奖金为 ,则
,则 是一个离散型随机变量.由于该工人每月完成任务与否是等可能的,所以他每月完成任务的概率等于
是一个离散型随机变量.由于该工人每月完成任务与否是等可能的,所以他每月完成任务的概率等于 . …………………2分
. …………………2分
所以,  ,
, ,
,
 ,
, . …………8分
. …………8分
 于是
于是 .
.
所以此工人在一个季度里所得奖金的期望为153. 75元. ……………………12分
18.解:(Ⅰ)取BC的中点H,连结PH, 连结AH交BD于E.
 . ……………………………2分
. ……………………………2分
又面 面
面 ,
, 面
面 .
.
 ,
, .
.
 ,
, .
.
 ,即
,即 . ………………………………………………4分
. ………………………………………………4分
因为AH为PA在平面 上的射影,
上的射影, . ……………………………6分
. ……………………………6分
(Ⅱ)连结PE,则由(Ⅰ)知 .
.
 为所求二面角的平面角. ……………………………………………8分
为所求二面角的平面角. ……………………………………………8分
在 中,由
中,由 ,求得
,求得 .
.
 .
.
即所求二面角的正切值为 . …………………………………………………12分
. …………………………………………………12分
另解:(Ⅰ)建系设点正确2分,求出两个法向量2分,判断正确2分;
(Ⅱ)求出两个法向量3分,求出余弦值2分,求出正切值1分.
19. 解:(Ⅰ)设 ,则
,则
 ,
,
 .
.
即点C的轨迹方程为 . …………………………………………………3分
. …………………………………………………3分
(Ⅱ) 由题意
由题意 .
.
 . ……………5分
. ……………5分
 .
.
 ,
,
 . ……………………………8分
. ……………………………8分
(Ⅲ) .
. .
.
 .
.
∴双曲线实轴长的取值范围是 . ………………………………………………12分
. ………………………………………………12分
20.解: (Ⅰ)由已知得 的定义域为
的定义域为 ,
, . ………………2分
. ………………2分
由题意得 对一切
对一切 恒成立,
恒成立,
 ……………………………………………5分
……………………………………………5分
当 时,
时, ,
,
 .故
.故 .
…………………………………………7分
.
…………………………………………7分
(Ⅱ)假设存在正实数 ,使得
,使得 成立.
成立.
 .
…………………9分
.
…………………9分
由 ,得
,得 ,
, .由于
.由于 ,故应舍去.
,故应舍去.
当 时,
时, ………………………………………11分
………………………………………11分
令 ,解得
,解得 或
或 . …………………………13分
. …………………………13分
另解: 假设存在正实数 ,使得
,使得 成立.
成立.
设 ,则
,则 . ………………………9分
. ………………………9分
由 ,解得
,解得 或
或 .
.
因为 ,
, 在
在 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
 . … ……………………………………11分
. … ……………………………………11分
令 ,解得
,解得 或
或 . …………………………13分
. …………………………13分
21.解:(Ⅰ)由已知 ,得
,得 .
.
则数列 是公比为2的等比数列. ……………………………………………2分
是公比为2的等比数列. ……………………………………………2分
又 . ……………………………………………4分
. ……………………………………………4分
(Ⅱ) . …………………6分
. …………………6分
 恒成立,则
恒成立,则


 解得
解得
故存在常数A,B,C,满足条件. …………………………………………9分
(Ⅲ)由(Ⅱ)知:


 . …………………14分
. …………………14分
=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com