
题目列表(包括答案和解析)
(本小题满分12分)
已知椭圆C: (常数
(常数 ),P是曲线C上的动点,M是曲线C的右
),P是曲线C上的动点,M是曲线C的右
顶点,定点A的坐标为(2,0).
(1)若M与A重合,求曲线C的焦点坐标.
(2)若 ,求|PA|的最大值与最小值.
,求|PA|的最大值与最小值.
(3)若|PA|最小值为|MA|,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知椭圆C: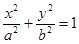 (a>b>0)的右焦点为F
(a>b>0)的右焦点为F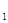 (1,0),离心率为
(1,0),离心率为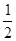 ,P为左顶点。
,P为左顶点。
(1)求椭圆C的方程;
(2)设过点F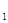 的直线交椭圆C于A,B两点,若△PAB的面积为
的直线交椭圆C于A,B两点,若△PAB的面积为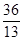 ,求直线AB的方程。
,求直线AB的方程。
(本小题满分12分)已知椭圆C: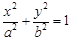 (
(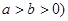 .
.
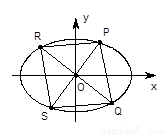
(1)若椭圆的长轴长为4,离心率为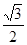 ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)在(1)的条件下,设过定点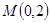 的直线
的直线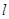 与椭圆C交于不同的两点
与椭圆C交于不同的两点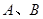 ,且
,且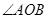 为锐角(其中
为锐角(其中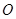 为坐标原点),求直线
为坐标原点),求直线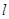 的斜率k的取值范围;
的斜率k的取值范围;
(3)如图,过原点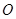 任意作两条互相垂直的直线与椭圆
任意作两条互相垂直的直线与椭圆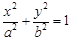 (
(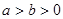 )相交于
)相交于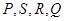 四点,设原点
四点,设原点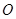 到四边形
到四边形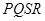 一边的距离为
一边的距离为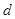 ,试求
,试求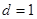 时
时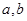 满足的条件.
满足的条件.
(本小题满分12分)
已知椭圆C: 的短轴长为
的短轴长为 ,且斜率为
,且斜率为 的直线
的直线 过椭圆C的焦点及点
过椭圆C的焦点及点 。
。
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知一直线 过椭圆C的左焦点
过椭圆C的左焦点 ,交椭圆于点P、Q,
,交椭圆于点P、Q,
(ⅰ)若满足 (
( 为坐标原点),求
为坐标原点),求 的面积;
的面积;
(ⅱ)若直线 与两坐标轴都不垂直,点M在
与两坐标轴都不垂直,点M在 轴上,且使
轴上,且使 为
为 的一条角平分线,则称点M为椭圆C的“左特征点”,求椭圆C的左特征点。
的一条角平分线,则称点M为椭圆C的“左特征点”,求椭圆C的左特征点。
(本小题满分12分)
已知椭圆C: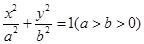 的离心率为
的离心率为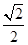 ,且过点Q(1,
,且过点Q(1,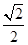 ).
).
(1) 求椭圆C的方程;
(2) 若过点M(2,0)的直线与椭圆C相交于A,B两点,设P点在直线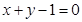
上,且满足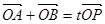 (O为坐标原点),求实数t的最小值.
(O为坐标原点),求实数t的最小值.
一、选择题
1-6 C A B B B D 7-12 B C B B B C
二、填空
13. 4 14. .files/image195.gif) 15. 2 16.
15. 2 16..files/image197.gif)
三、解答题
17.(1)解:由.files/image199.gif)
有.files/image201.gif) ……6分
……6分
由.files/image203.gif) , ……8分
, ……8分
由余弦定理.files/image205.gif)
当.files/image207.gif) ……12分
……12分
.files/image208.jpg) ∴PB∥平面EFG. ………………………………3分
∴PB∥平面EFG. ………………………………3分
(2)解:取BC的中点M,连结GM、AM、EM,则GM//BD,
|