
题目列表(包括答案和解析)
| 1 | 2 |
| 3 | 4 |
| 文具 | 计算器 |
| 计算器 | 海宝 |

| 1 | 2 |
| 3 | 4 |
| 文具 | 计算器 |
| 计算器 | 海宝 |
先阅读,再利用其结论解决问题.
阅读:已知一元二次方程ax2+bx+c=0(a≠0)的两个实根为x1,x2,则有x1+x2=﹣,x1•x2=.这个结论是法国数学家韦达最先发现并证明的,故把它称为“韦达定理”.利用此定理,可以不解方程就得出x1+x2和 x1•x2的值,进而求出相关的代数式的值.
解决问题:对于一切不小于2的自然数n,关于x的一元二次方程x2﹣(n+2)x﹣2n2=0的两个根记作an,bn(n≥2),
请求出
![]()
![]() +…
+…![]() 的值.
的值.
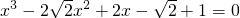 ,这是一个高次方程,我们未学过其解法,难以求解.如果我们换一个角度(“已知”和“未知”互换),即将
,这是一个高次方程,我们未学过其解法,难以求解.如果我们换一个角度(“已知”和“未知”互换),即将 看做“未知数”,而将x看成“已知数”,则原方程可整理成:
看做“未知数”,而将x看成“已知数”,则原方程可整理成: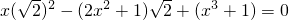 .
.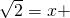 1或
1或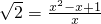 .
.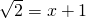 和一个一元二次方程x2-x+1=
和一个一元二次方程x2-x+1= ,从而不难求得这个高次方程的解.
,从而不难求得这个高次方程的解.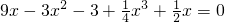 .
.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com