
题目列表(包括答案和解析)
| |||||||||||
解:能否投中,那得看抛物线与篮圈所在直线是否有交点。因为函数![]() 的零点是-2与4,篮圈所在直线x=5在4的右边,抛物线又是开口向下的,所以投不中。
的零点是-2与4,篮圈所在直线x=5在4的右边,抛物线又是开口向下的,所以投不中。
某城市出租汽车的起步价为10元,行驶路程不超出4km,则按10元的标准收租车费![]() 若行驶路程超出4km,则按每超出lkm加收2元计费(超出不足1km的部分按lkm计).从这个城市的民航机场到某宾馆的路程为15km.某司机常驾车在机场与此宾馆之间接送旅客,由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定,每停车5分钟按lkm路程计费),这个司机一次接送旅客的行车路程ξ是一个随机变量,
若行驶路程超出4km,则按每超出lkm加收2元计费(超出不足1km的部分按lkm计).从这个城市的民航机场到某宾馆的路程为15km.某司机常驾车在机场与此宾馆之间接送旅客,由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定,每停车5分钟按lkm路程计费),这个司机一次接送旅客的行车路程ξ是一个随机变量,
(1)他收旅客的租车费η是否也是一个随机变量?如果是,找出租车费η与行车路程ξ的关系式;
(2)已知某旅客实付租车费38元,而出租汽车实际行驶了15km,问出租车在途中因故停车累计最多几分钟?这种情况下,停车累计时间是否也是一个随机变量?
如图所示,圆柱的高为2,底面半径为 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过 作圆柱的截面交下底面于
作圆柱的截面交下底面于 .
.
(1)求证: ;
;
(2)若四边形ABCD是正方形,求证 ;
;
(3)在(2)的条件下,求二面角A-BC-E的平面角的一个三角函数值。

【解析】第一问中,利用由圆柱的性质知:AD平行平面BCFE
又过 作圆柱的截面交下底面于
作圆柱的截面交下底面于 .
. ∥
∥
又AE、DF是圆柱的两条母线
 ∥DF,且AE=DF
∥DF,且AE=DF  AD∥EF
AD∥EF
第二问中,由线面垂直得到线线垂直。四边形ABCD是正方形
 又
又
BC、AE是平面ABE内两条相交直线



第三问中,设正方形ABCD的边长为x,则在
在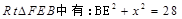

由(2)可知: 为二面角A-BC-E的平面角,所以
为二面角A-BC-E的平面角,所以
证明:(1)由圆柱的性质知:AD平行平面BCFE
又过 作圆柱的截面交下底面于
作圆柱的截面交下底面于 .
. ∥
∥
又AE、DF是圆柱的两条母线
 ∥DF,且AE=DF
∥DF,且AE=DF  AD∥EF
AD∥EF

(2) 四边形ABCD是正方形
四边形ABCD是正方形
 又
又
BC、AE是平面ABE内两条相交直线



(3)设正方形ABCD的边长为x,则在
在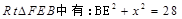

由(2)可知: 为二面角A-BC-E的平面角,所以
为二面角A-BC-E的平面角,所以
已知向量 ,且
,且 ,A为锐角,求:
,A为锐角,求:
(1)角A的大小;
(2)求函数 的单调递增区间和值域.
的单调递增区间和值域.
【解析】第一问中利用 ,解得
,解得 又A为锐角
又A为锐角

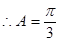
第二问中,
由 解得单调递增区间为
解得单调递增区间为
解:(1) ……………………3分
……………………3分
 又A为锐角
又A为锐角

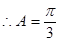 ……………………5分
……………………5分
(2)
……………………8分
由 解得单调递增区间为
解得单调递增区间为
……………………10分

在数列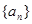 中,
中,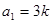 ,其中
,其中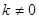 ,对任意
,对任意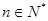 都有:
都有: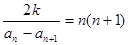 ;(1)求数列
;(1)求数列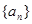 的第2项和第3项;
的第2项和第3项;
(2)求数列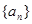 的通项公式
的通项公式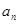 ,假设
,假设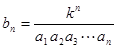 ,试求数列
,试求数列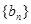 的前
的前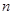 项和
项和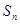 ;
;
(3)若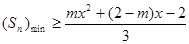 对一切
对一切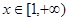 恒成立,求
恒成立,求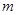 的取值范围。
的取值范围。
【解析】第一问中利用)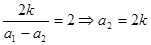 同理得到
同理得到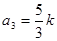
第二问中,由题意得到: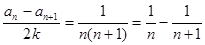
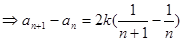
累加法得到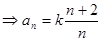
第三问中,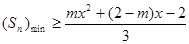 利用恒成立,转化为最小值大于等于即可。得到范围。
利用恒成立,转化为最小值大于等于即可。得到范围。
(1)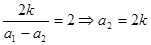 同理得到
同理得到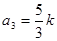 ……2分
……2分
(2)由题意得到: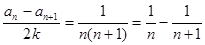
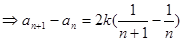
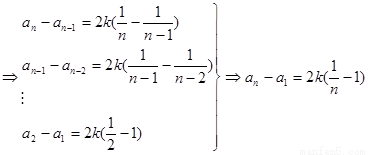 又
又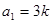
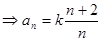 ……5分
……5分
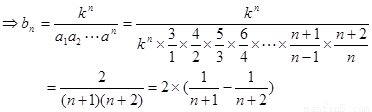
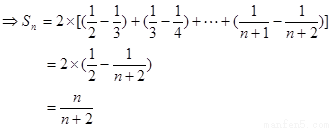 ……8分
……8分
(3)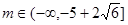
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com