
题目列表(包括答案和解析)
已知实数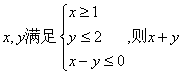 的最小值为 ( )
的最小值为 ( )
A.2 B.3 C.4 D.5
已知函数![]() 的最小值为
的最小值为![]()
(Ⅰ)求![]()
(Ⅱ)是否存在实数m,n同时满足下列条件:
①m>n>3;
②当![]() 的定义域为[n,m]时,值域为[n2,m2]?
的定义域为[n,m]时,值域为[n2,m2]?
若存在,求出m,n的值;若不存在,说明理由.
已知函数![]() 的最小值为
的最小值为![]()
(Ⅰ)求![]()
(Ⅱ)是否存在实数m,n同时满足下列条件:
① m>n>3;
② ②当![]() 的定义域为[n,m]时,值域为[n2,m2]?
的定义域为[n,m]时,值域为[n2,m2]?
若存在,求出m,n的值;若不存在,说明理由.
已知函数 的最小值为0,其中
的最小值为0,其中 。
。
(1)求a的值
(2)若对任意的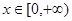 ,有
,有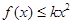 成立,求实数k的最小值
成立,求实数k的最小值
(3)证明
已知函数 的最小值为0,其中
的最小值为0,其中
(Ⅰ)求 的值;
的值;
(Ⅱ)若对任意的 有
有 ≤
≤ 成立,求实数
成立,求实数 的最小值;
的最小值;
(Ⅲ)证明 (
( ).
).
【解析】(1)解:
 的定义域为
的定义域为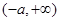

由 ,得
,得
当x变化时, ,
, 的变化情况如下表:
的变化情况如下表:
|
x |
|
|
|
|
|
- |
0 |
+ |
|
|
|
极小值 |
|
因此, 在
在 处取得最小值,故由题意
处取得最小值,故由题意 ,所以
,所以
(2)解:当 时,取
时,取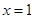 ,有
,有 ,故
,故 时不合题意.当
时不合题意.当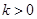 时,令
时,令 ,即
,即

令 ,得
,得
①当 时,
时, ,
, 在
在 上恒成立。因此
上恒成立。因此 在
在 上单调递减.从而对于任意的
上单调递减.从而对于任意的 ,总有
,总有 ,即
,即 在
在 上恒成立,故
上恒成立,故 符合题意.
符合题意.
②当 时,
时, ,对于
,对于 ,
, ,故
,故 在
在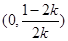 上单调递增.因此当取
上单调递增.因此当取 时,
时, ,即
,即 不成立.
不成立.
故 不合题意.
不合题意.
综上,k的最小值为 .
.
(3)证明:当n=1时,不等式左边= =右边,所以不等式成立.
=右边,所以不等式成立.
当 时,
时,


在(2)中取 ,得
,得
 ,
,
从而

所以有





综上,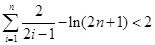 ,
,
一、选择题:本大题共12小题,每小题5分,共60分。
1―5 DBCDC 6―10BBCAB 11―12 DB
二、填空题:本大题共4小题,每小题4分,共16分。
13.“ ” 14.
” 14. 15.1200 16.
15.1200 16.
三、解答题:本大题共6小题,共80分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分13分)
解:(I)由已知

(II)

|