设a=2－，b=－2，c=5－2，写出a、b、c的大小关系___________.

查看答案和解析>>

查看答案和解析>>

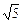设a=2－，b=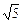－2，c=5－2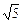，则a、b、c之间的大小关系为____________.

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

难点磁场

解：原不等式可化为：＞0，

即［(a－1)x+(2－a)］(x－2)＞0.

当a＞1时，原不等式与(x－)(x－2)＞0同解.

若≥2，即0≤a＜1时，原不等式无解；若＜2，即a＜0或a＞1，于是a＞1时原不等式的解为(－∞，)∪(2，+∞).

当a＜1时，若a＜0，解集为(，2)；若0＜a＜1，解集为(2，)

综上所述：当a＞1时解集为(－∞，)∪(2，+∞)；当0＜a＜1时，解集为(2，)；当a=0时，解集为；当a＜0时，解集为(，2）.

歼灭难点训练

一、1.解析：由f(x)及f(a)＞1可得：

    ①  或   ②  或   ③

解①得a＜－2，解②得－＜a＜1，解③得x∈

∴a的取值范围是(－∞，－2)∪(－，1）

答案：C

二、

2.解析：由已知b＞a²∵f(x)，g(x)均为奇函数，∴f(x)＜0的解集是(－b，－a²)，g(x)＜0的解集是(－).由f(x)?g(x)＞0可得：

∴x∈(a²，)∪(－，－a²)

答案：(a²，)∪(－，－a²)

3.解析：原方程可化为cos²x－2cosx－a－1=0，令t=cosx，得t²－2t－a－1=0，原问题转化为方程t²－2t－a－1=0在［－1，1］上至少有一个实根.令f(t)=t²－2t－a－1，对称轴t=1，画图象分析可得解得a∈［－2，2］.

答案：［－2，2］

三、

4.解：(1)∵适合不等式|x²－4x+p|+|x－3|≤5的x的最大值为3，

∴x－3≤0，∴|x－3|=3－x.

若|x²－4x+p|=－x²+4x－p，则原不等式为x²－3x+p+2≥0，其解集不可能为{x|x≤3}的子集，∴|x²－4x+p|=x²－4x+p.

∴原不等式为x²－4x+p+3－x≤0，即x²－5x+p－2≤0，令x²－5x+p－2=(x－3)(x－m)，可得m=2，p=8.

(2)f(x)=，∴f^-－1(x)=log₈ (－1＜x＜1，

∴有log₈＞log₈，∴log₈(1－x)＜log₈k，∴1－x＜k，∴x＞1－k.

∵－1＜x＜1，k∈R⁺，∴当0＜k＜2时，原不等式解集为{x|1－k＜x＜1}；当k≥2时，原不等式的解集为{x|－1＜x＜1.

5.解：由f(1)=得a+b+c=，令x²+=2x²+2x+x=－1，由f(x)≤2x²+2x+推得

f(－1)≤.

由f(x)≥x²+推得f(－1)≥，∴f(－1)=，∴a－b+c=，故

2(a+c)=5，a+c=且b=1，∴f(x)=ax²+x+(－a).

依题意：ax²+x+(－a)≥x²+对一切x∈R成立，

∴a≠1且Δ=1－4(a－1)(2－a)≤0，得(2a－3)²≤0，

∴f(x)=x²+x+1

易验证：x²+x+1≤2x²+2x+对x∈R都成立.

∴存在实数a=，b=1，c=1，使得不等式：x²+≤f(x)≤2x²+2x+对一切x∈R都成立.

6.解：(1)∵－1≤sinθ≤1，1≤sinθ+2≤3，即当x∈［－1，1］时，f(x)≤0，当x∈［1，3］时，f(x)≥0，∴当x=1时f(x)=0.∴1+p+q=0，∴q=－(1+p)

(2)f(x)=x²+px－(1+p)，

当sinθ=－1时f(－1)≤0，∴1－p－1－p≤0，∴p≥0

(3)注意到f(x)在［1，3］上递增，∴x=3时f(x)有最大值.即9+3p+q=14，9+3p－1－p=14，∴p=3.

此时，f(x)=x²+3x－4，即求x∈［－1，1］时f(x)的最小值.又f(x)=(x+)²－，显然此函数在［－1，1］上递增.

∴当x=－1时f(x)有最小值f(－1)=1－3－4=－6.

7.解：(1)当a＞1时，原不等式等价于不等式组

由此得1－a＞.因为1－a＜0，所以x＜0，∴＜x＜0.

(2)当0＜a＜1时，原不等式等价于不等式组：                     

由 ①得x＞1或x＜0，由②得0 ＜x＜，∴1＜x＜.

综上，当a＞1时，不等式的解集是{x|＜x＜0，当0＜a＜1时，不等式的解集为{x|1＜x＜}.

8.解：由已知得0＜a＜1，由f(3mx－1)＞f(1+mx－x²)＞f(m+2)，x∈(0，1恒成立.

在x∈(0，1恒成立.

整理，当x∈(0，1)时，恒成立，即当x∈(0，1时，恒成立，且x=1时，恒成立，

∵在x∈(0，1上为减函数，∴＜－1，

∴m＜恒成立m＜0.

又∵，在x∈(0，1上是减函数，?

∴＜－1.

∴m＞恒成立m＞－1当x∈(0，1)时，恒成立m∈(－1，0)①

当x=1时，，即是∴m＜0                                                 ②

∴①、②两式求交集m∈(－1，0）,使x∈(0，1时，f(3mx－1)＞f(1+mx－x²)＞f(m+2)恒成立，m的取值范围是(－1，0)