
题目列表(包括答案和解析)
(本小题满分14分)
设![]() 是把坐标平面上点的横坐标不变、纵坐标沿
是把坐标平面上点的横坐标不变、纵坐标沿![]() 轴方向伸长为原来5倍的伸压变换.
轴方向伸长为原来5倍的伸压变换.
(1)求直线![]() 在
在![]() 作用下的方程;
作用下的方程;
(2)求![]() 的特征值与特征向量.
的特征值与特征向量.
(本小题满分10分)
已知一条曲线上的点到定点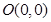 的距离是到定点
的距离是到定点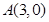 距离的二倍,求这条曲线的方程.
距离的二倍,求这条曲线的方程.
(本小题满分12分)
已知 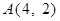 ,
, ,
,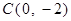 为坐标平面上的三个点,
为坐标平面上的三个点,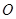 为坐标原点,点
为坐标原点,点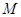 为
为 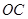 所在直线上一个动点.
所在直线上一个动点.
(Ⅰ)若 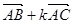 与
与 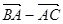 垂直,求
垂直,求 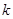 的值;
的值;
(Ⅱ)若向量 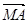 在向量
在向量  方向上的射影的数量为
方向上的射影的数量为 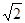 ,求
,求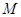 点的坐标.
点的坐标.
(本小题满分16分)
设![]() 是定义在区间
是定义在区间![]() 上的函数,其导函数为
上的函数,其导函数为![]() 。如果存在实数
。如果存在实数![]() 和函数
和函数![]() ,其中
,其中![]() 对任意的
对任意的![]() 都有
都有![]() >0,使得
>0,使得![]() ,则称函数
,则称函数![]() 具有性质
具有性质![]() 。
。
(1)设函数![]()
![]() ,其中
,其中![]() 为实数。
为实数。
(i)求证:函数![]() 具有性质
具有性质![]() ; (ii)求函数
; (ii)求函数![]() 的单调区间。
的单调区间。
(2)已知函数![]() 具有性质
具有性质![]() 。给定
。给定![]() 设
设![]() 为实数,
为实数,
![]() ,
,![]() ,且
,且![]() ,
,
若|![]() |<|
|<|![]() |,求
|,求![]() 的取值范围。
的取值范围。
(本小题满分10分)设函数 (其中
(其中 >
>
0, ),且
),且 的图象在y轴右侧的第一个最高点的横坐标为
的图象在y轴右侧的第一个最高点的横坐标为 .
.
(1)求 的最小正周期;
的最小正周期;
(2)如果 在区间
在区间 上的最小值为
上的最小值为 ,求a的值.
,求a的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com