
题目列表(包括答案和解析)
(本题满分14分)
甲打靶射击,有4发子弹,其中有一发是空弹.
(1)求空弹出现在第一枪的概率;
(2)求空弹出现在前三枪的概率;
(3)如果把空弹换成实弹,甲前三枪在靶上留下三个两两距离分别为3,4,5的弹孔 ,第四枪瞄准了三角形
,第四枪瞄准了三角形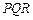 射击,第四个弹孔落在三角形
射击,第四个弹孔落在三角形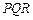 内
内 ,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
(本题满分14分)
甲打靶射击,有4发子弹,其中有一发是空弹.
(1)求空弹出现在第一枪的概率;
(2)求空弹出现在前三枪的概率;
(3)如果把空弹换成实弹,甲前三枪在靶上留下三个两两距离分别为3,4,5的弹孔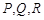 ,第四枪瞄准了三角形
,第四枪瞄准了三角形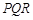 射击,第四个弹孔落在三角形
射击,第四个弹孔落在三角形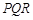 内,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
内,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
(本题满分14分,第1小题5分,第2小题9分)
一校办服装厂花费2万元购买某品牌运动装的生产与销售权,根据以往经验,每生产1百套这种品牌运动装的成本为1万元,每生产x(百套)的销售额R(x)(万元)满足:

(1)该服装厂生产750套此种品牌运动装可获得利润多少万元?
(2)该服装厂生产多少套此种品牌运动装利润最大?此时,利润是多少万元?
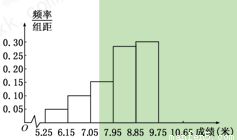
(本题满分12分)某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
( I ) 求这次铅球测试成绩合格的人数;
(II) 用此次测试结果估计全市毕业生的情况.若从今年的高中毕业生中随机抽取两名,记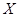 表示两人中成绩不合格的人数,求
表示两人中成绩不合格的人数,求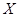 的数学期望和方差.
的数学期望和方差.
(本题满分14分,第1小题5分,第2小题9分)
已知![]() ,
,![]() ,
,![]() .
.
⑴若![]() ∥
∥![]() ,求
,求![]() 的值;
的值;
⑵若![]() ,求
,求![]() 的值.
的值.
一、填空题2009.03.files/image132.gif) (每题5分)
(每题5分)
1)2009.03.files/image134.gif) 2)
2)2009.03.files/image136.gif) 3)0 4)
3)0 4)2009.03.files/image138.gif) 5)
5)2009.03.files/image140.gif) 6) ②④ 7)
6) ②④ 7)2009.03.files/image142.gif) 8)
8)2009.03.files/image144.gif) 9)
9)2009.03.files/image146.gif) 10)
10)2009.03.files/image148.gif) 11)
11)2009.03.files/image150.gif)
二、选择题 (每题5分)
2009.03.files/image151.jpg) 12、A 13、B 14、B 15、D
12、A 13、B 14、B 15、D
三、解答题
16、
(1)因为2009.03.files/image153.gif) ,所以∠BCA(或其补角)即为异面直线
,所以∠BCA(或其补角)即为异面直线2009.03.files/image155.gif) 与
与2009.03.files/image157.gif) 所成角
-------(3分)
所成角
-------(3分)
∠ABC=90°, AB=BC=1,所以2009.03.files/image159.gif) ,
-------(2分)
,
-------(2分)
即异面直线2009.03.files/image155.gif) 与
与2009.03.files/image157.gif) 所成角大小为
所成角大小为2009.03.files/image018.gif) 。
-------(1分)
。
-------(1分)
(2)直三棱柱ABC-A1B2009.03.files/image162.gif) ,所以
,所以2009.03.files/image164.gif) 即为直线A
即为直线A2009.03.files/image166.gif) 。 -------(2分)
。 -------(2分)
2009.03.files/image168.gif) 中,AB=BC=1得到
中,AB=BC=1得到2009.03.files/image170.gif) ,
,2009.03.files/image172.gif) 中,得到
中,得到2009.03.files/image174.gif) , -------(2分)
, -------(2分)
所以2009.03.files/image176.gif) -------(2分)
-------(2分)
17、(102009.03.files/image085.gif) =
=2009.03.files/image178.gif) -------(1分)
-------(1分)
=2009.03.files/image180.gif) -------(1分)
-------(1分)
=2009.03.files/image182.gif) -------(1分)
-------(1分)
周期2009.03.files/image184.gif) ; -------(1分)
; -------(1分)
2009.03.files/image186.gif) ,解得单调递增区间为
,解得单调递增区间为2009.03.files/image188.gif) -------(2分)
-------(2分)
(2)2009.03.files/image092.gif) ,所以
,所以2009.03.files/image190.gif) ,
,
2009.03.files/image192.gif) ,
,
所以2009.03.files/image064.gif) 的值域为
的值域为2009.03.files/image195.gif) ,
-------(4分)
,
-------(4分)
而2009.03.files/image197.gif) ,所以
,所以2009.03.files/image199.gif) ,即
,即2009.03.files/image201.gif) -------(4分)
-------(4分)
18、2009.03.files/image203.gif) ,顾客得到的优惠率是
,顾客得到的优惠率是2009.03.files/image205.gif) 。 -------(5分)
。 -------(5分)
(2)、设商品的标价为x元,则500≤x≤800 ------(2分)
消费金额: 400≤0.8x≤640
由题意可得:
(1)2009.03.files/image206.jpg) ≥
≥2009.03.files/image207.jpg) 无解
------(3分)
无解
------(3分)
或(2)2009.03.files/image208.jpg) ≥
≥2009.03.files/image207.jpg) 得:625≤x≤750 ------(3分)
得:625≤x≤750 ------(3分)
因此,当顾客购买标价在2009.03.files/image209.jpg) 元内的商品时,可得到不小于
元内的商品时,可得到不小于2009.03.files/image207.jpg) 的优惠率。------(1分)
的优惠率。------(1分)
19、(1)2009.03.files/image102.gif) 与
与2009.03.files/image088.gif) 轴的交点
轴的交点2009.03.files/image212.gif) 为
为2009.03.files/image214.gif) , ------(1分)
, ------(1分)
2009.03.files/image216.gif) ;所以
;所以2009.03.files/image218.gif) ,即
,即2009.03.files/image220.gif) ,-
----(1分)
,-
----(1分)
因为2009.03.files/image222.gif) 在
在2009.03.files/image102.gif) 上,所以
上,所以2009.03.files/image224.gif) ,即
,即2009.03.files/image226.gif) ----(2分)
----(2分)
(2)若2009.03.files/image111.gif)
2009.03.files/image113.gif) (
(2009.03.files/image115.gif) ),
),
即若2009.03.files/image228.gif)
2009.03.files/image113.gif) (
(2009.03.files/image115.gif) ) ----(1分)
) ----(1分)
(A)当2009.03.files/image232.gif) 时,
时,2009.03.files/image234.gif)
2009.03.files/image236.gif) ----(1分)
----(1分)
=2009.03.files/image238.gif) =
=2009.03.files/image240.gif) ,而
,而2009.03.files/image242.gif) ,所以
,所以2009.03.files/image244.gif) ----(1分)
----(1分)
(B)当2009.03.files/image246.gif) 时,
时,2009.03.files/image248.gif) ----(1分)
----(1分)
= 2009.03.files/image250.gif) =
=2009.03.files/image252.gif) ,
----(1分)
,
----(1分)
而2009.03.files/image254.gif) ,所以
,所以2009.03.files/image256.gif) ----(1分)
----(1分)
因此2009.03.files/image258.gif) (
(2009.03.files/image115.gif) )
----(1分)
)
----(1分)
(3)假设存在2009.03.files/image127.gif) 使得
使得2009.03.files/image261.gif) 成立。
成立。
(A)若2009.03.files/image127.gif) 为奇数,则
为奇数,则2009.03.files/image264.gif) 为偶数。所以
为偶数。所以2009.03.files/image266.gif) ,
,2009.03.files/image268.gif) ,而
,而2009.03.files/image261.gif) ,所以
,所以2009.03.files/image270.gif) ,方程无解,此时不存在。 ----(2分)
,方程无解,此时不存在。 ----(2分)
(B) 若2009.03.files/image127.gif) 为偶数,则
为偶数,则2009.03.files/image264.gif) 为奇数。所以
为奇数。所以2009.03.files/image272.gif) ,
,2009.03.files/image274.gif) ,而
,而2009.03.files/image261.gif) ,所以
,所以2009.03.files/image276.gif) ,解得
,解得2009.03.files/image278.gif) ----(2分)
----(2分)
由(A)(B)得存在2009.03.files/image280.gif) 使得
使得2009.03.files/image261.gif) 成立。
----(1分)
成立。
----(1分)
20、(1)(A):点P与点F(2,0)的距离比它到直线2009.03.files/image088.gif) +4=0的距离小2,所以点P与点F(2,0)的距离与它到直线
+4=0的距离小2,所以点P与点F(2,0)的距离与它到直线2009.03.files/image088.gif) +2=0的距离相等。 ----(1分)
+2=0的距离相等。 ----(1分)
由抛物线定义得:点2009.03.files/image282.gif) 在以
在以2009.03.files/image284.gif) 为焦点直线
为焦点直线2009.03.files/image088.gif) +2=0为准线的抛物线上, ----(1分)
+2=0为准线的抛物线上, ----(1分)
抛物线方程为2009.03.files/image286.gif) 。 ----(2分)
。 ----(2分)
解法(B):设动点2009.03.files/image288.gif) ,则
,则2009.03.files/image290.gif) 。当
。当2009.03.files/image292.gif) 时,
时,2009.03.files/image294.gif) ,化简得:
,化简得:2009.03.files/image296.gif) ,显然
,显然2009.03.files/image298.gif) ,而
,而2009.03.files/image292.gif) ,此时曲线不存在。当
,此时曲线不存在。当2009.03.files/image136.gif) 时,
时,2009.03.files/image301.gif) ,化简得:
,化简得:2009.03.files/image286.gif) 。
。
(2)2009.03.files/image303.gif) ,
,
2009.03.files/image305.gif) ,
,
2009.03.files/image307.gif) ,
----(1分)
,
----(1分)
2009.03.files/image309.gif) ,
,
2009.03.files/image311.gif) ,即
,即2009.03.files/image313.gif) ,
,2009.03.files/image315.gif) ,
----(2分)
,
----(2分)
直线为2009.03.files/image317.gif) ,所以
,所以2009.03.files/image319.gif) ----(1分)
----(1分)
2009.03.files/image321.gif)
2009.03.files/image323.gif) ----(1分)
----(1分)
由(a)(b)得:直线恒过定点2009.03.files/image325.gif) 。
----(1分)
。
----(1分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com