
题目列表(包括答案和解析)
设函数 ,若
,若 为函数
为函数 的一个极值点,则下列图象不可能为
的一个极值点,则下列图象不可能为 的图象是
的图象是

【答案】D
【解析】设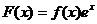 ,∴
,∴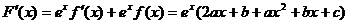 ,
,
又∴ 为
为 的一个极值点,
的一个极值点,
∴ ,即
,即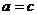 ,
,
∴ ,
,
当 时,
时, ,即对称轴所在直线方程为
,即对称轴所在直线方程为 ;
;
当 时,
时, ,即对称轴所在直线方程应大于1或小于-1.
,即对称轴所在直线方程应大于1或小于-1.
【答案】![]()
【解析】设![]() ,有几何意义知
,有几何意义知![]() 的最小值为
的最小值为![]() , 又因为存在实数x满足
, 又因为存在实数x满足![]() ,所以只要2大于等于f(x)的最小值即可.即
,所以只要2大于等于f(x)的最小值即可.即![]() 2,解得:
2,解得:![]() ∈
∈![]() ,所以a的取值范围是
,所以a的取值范围是![]() .故答案为:
.故答案为:![]() .
.
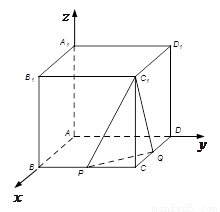
如图,在正方体 中,
中,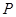 是棱
是棱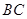 的中点,
的中点,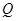 在棱
在棱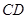 上.
上.
且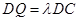 ,若二面角
,若二面角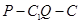 的余弦值为
的余弦值为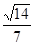 ,求实数
,求实数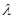 的值.
的值.
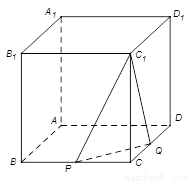
【解析】以A点为坐标原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,设正方体的棱长为4,分别求出平面C1PQ法向量和面C1PQ的一个法向量,然后求出两法向量的夹角,建立等量关系,即可求出参数λ的值.
设函数 .
.
(I)求 的单调区间;
的单调区间;
(II)当0<a<2时,求函数 在区间
在区间 上的最小值.
上的最小值.
【解析】第一问定义域为真数大于零,得到 .
. .
.
令 ,则
,则 ,所以
,所以 或
或 ,得到结论。
,得到结论。
第二问中, (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .
.
对参数讨论的得到最值。
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
(I)定义域为 . ………………………1分
. ………………………1分
 .
.
令 ,则
,则 ,所以
,所以 或
或 . ……………………3分
. ……………………3分
因为定义域为 ,所以
,所以 .
.
令 ,则
,则 ,所以
,所以 .
.
因为定义域为 ,所以
,所以 . ………………………5分
. ………………………5分
所以函数的单调递增区间为 ,
,
单调递减区间为 .
………………………7分
.
………………………7分
(II) (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .…………9分
.…………9分
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
①当 ,即
,即 时,
时,
在区间 上,
上, 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
所以 . ………………………10分
. ………………………10分
②当 ,即
,即 时,
时, 在区间
在区间 上为减函数.
上为减函数.
所以 .
.
综上所述,当 时,
时, ;
;
当 时,
时,
如图,直线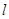 与抛物线
与抛物线 交于
交于 两点,与
两点,与 轴相交于点
轴相交于点 ,且
,且 .
.
(1)求证: 点的坐标为
点的坐标为 ;
;
(2)求证: ;
;
(3)求 的面积的最小值.
的面积的最小值.

【解析】设出点M的坐标 ,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为
,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为 ,然后与抛物线方程联立消x,根据
,然后与抛物线方程联立消x,根据 ,即可建立关于
,即可建立关于 的方程.求出
的方程.求出 的值.
的值.
(2)在第(1)问的基础上,证明: 即可.
即可.
(3)先建立面积S关于m的函数关系式,根据 建立即可,然后再考虑利用函数求最值的方法求最值.
建立即可,然后再考虑利用函数求最值的方法求最值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com