
题目列表(包括答案和解析)
设函数![]() 的两个零点分别是-3和2;
的两个零点分别是-3和2;
(1)求![]() ;
;
(2)当函数![]() 的定义域是[0,1]时,求函数
的定义域是[0,1]时,求函数![]() 的值域。
的值域。
设双曲线 的两个焦点分别为
的两个焦点分别为 、
、 ,离心率为2.
,离心率为2.
(1)求双曲线的渐近线方程;
(2)过点 能否作出直线
能否作出直线 ,使
,使 与双曲线
与双曲线 交于
交于 、
、 两点,且
两点,且 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由.
【解析】(1)根据离心率先求出a2的值,然后令双曲线等于右侧的1为0,解此方程可得双曲线的渐近线方程.
(2)设直线l的方程为 ,然后直线方程与双曲线方程联立,消去y,得到关于x的一元二次方程,利用韦达定理
,然后直线方程与双曲线方程联立,消去y,得到关于x的一元二次方程,利用韦达定理 表示此条件,得到关于k的方程,解出k的值,然后验证判别式是否大于零即可.
表示此条件,得到关于k的方程,解出k的值,然后验证判别式是否大于零即可.
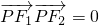 ,
,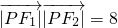 .
.| PF1 |
| PF2 |
| |PF1| |
| |PF2| |
![]() =0,
=0,![]() =8.
=8.
(Ⅰ)求椭圆M的方程;
(Ⅱ)点A是椭圆M短轴的一个端点,且其纵坐标大于零,B、C是椭圆M上不同于点A的两点.若△ABC的重心是椭圆M的右焦点,求直线BC的方程.
一、选择题:
|