
题目列表(包括答案和解析)
在等式cos2x=2cos2x-1(x∈R)的两边求导,得:![]() ,由求导法则,得(-sin2x)·2=4cosx·(-sinx),化简得等式:sin2x=2cosx·sinx.
,由求导法则,得(-sin2x)·2=4cosx·(-sinx),化简得等式:sin2x=2cosx·sinx.
(1)利用上题的想法(或其他方法),结合等式![]() (x∈R,正整数n≥2),证明:
(x∈R,正整数n≥2),证明:![]() .
.
(2)对于正整数n≥3,求证:
(i)![]() ;
;
(ii)![]() ;
;
(iii)![]() .
.
请先阅读:在等式cos2x=2cos2x-1(x∈R)的两边求导,得:
![]() ,
,
由求导法则,得(-sin2x)·2=4cosx·(-sinx),化简得等式:sin2x=2cosx·sinx.
(1)利用上题的想法(或其他方法),试由等式(1+x)n=![]() (x∈R,正整数n≥2),证明:n[(1+x)n-1-1]=
(x∈R,正整数n≥2),证明:n[(1+x)n-1-1]=![]() .
.
(2)对于正整数n≥3,求证:
(i)![]() =0;
=0;
(ii)![]() =0;
=0;
(iii)![]() .
.
(2010·北京理,15)已知函数f(x)=2cos2x+sin2x-4cosx.
(1)求f(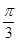 )的值;
)的值;
(2)求f(x)的最大值和最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com