
题目列表(包括答案和解析)
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| 尺寸 | [2.7,2.8] | (2.8,2.9] | (2.9,3.0] | (3.0,3.1] | (3.1,3.2] | (3.2,3.3] |
| 甲机床零件频数 | 2 | 3 | 20 | 20 | 4 | 1 |
| 乙机床零件频数 | 3 | 5 | 17 | 13 | 8 | 4 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
7、9、10班同学做乙题,其他班同学任选一题,若两题都做,则以较少得分计入总分.
(甲)已知f(x)=ax-ln(-x),x∈[-e,0),![]() ,其中e=2.718 28…是自然对数的底数,a∈R.
,其中e=2.718 28…是自然对数的底数,a∈R.
(1)若a=-1,求f(x)的极值;
(2)求证:在(1)的条件下,![]() ;
;
(3)是否存在实数a,使f(x)的最小值是3,如果存在,求出a的值;如果不存在,说明理由.
(乙)定义在(0,+∞)上的函数![]() ,其中e=2.718 28…是自然对数的底数,a∈R.
,其中e=2.718 28…是自然对数的底数,a∈R.
(1)若函数f(x)在点x=1处连续,求a的值;
(2)若函数f(x)为(0,1)上的单调函数,求实数a的取值范围;并判断此时函数f(x)在(0,+∞)上是否为单调函数;
(3)当x∈(0,1)时,记g(x)=lnf(x)+x2-ax. 试证明:对![]() ,当n≥2时,有
,当n≥2时,有![]()
已知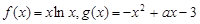
(1)求函数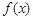 在
在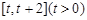 上的最小值
上的最小值
(2)对一切的 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
(3)证明对一切 ,都有
,都有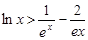 成立
成立
【解析】第一问中利用
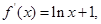 当
当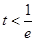 时,
时,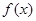 在
在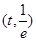 单调递减,在
单调递减,在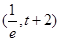 单调递增
单调递增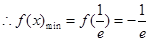 ,当
,当
 ,即
,即 时,
时,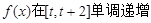 ,
,
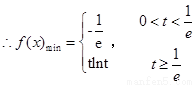
第二问中,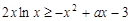 ,则
,则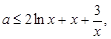 设
设 ,
,
则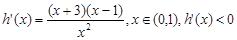 ,
, 单调递增,
单调递增, ,
, ,
, 单调递减,
单调递减,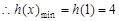 ,因为对一切
,因为对一切 ,
,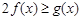 恒成立,
恒成立,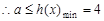
第三问中问题等价于证明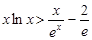 ,
, ,
,
由(1)可知 ,
, 的最小值为
的最小值为 ,当且仅当x=
,当且仅当x= 时取得
时取得
设 ,
, ,则
,则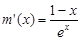 ,易得
,易得
 。当且仅当x=1时取得.从而对一切
。当且仅当x=1时取得.从而对一切 ,都有
,都有 成立
成立
解:(1)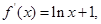 当
当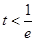 时,
时,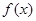 在
在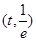 单调递减,在
单调递减,在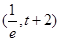 单调递增
单调递增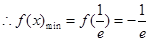 ,当
,当
 ,即
,即 时,
时,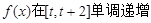 ,
,
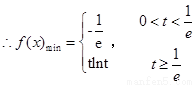 …………4分
…………4分
(2)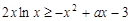 ,则
,则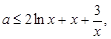 设
设 ,
,
则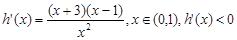 ,
, 单调递增,
单调递增, ,
, ,
, 单调递减,
单调递减,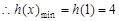 ,因为对一切
,因为对一切 ,
,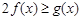 恒成立,
恒成立,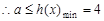 …………9分
…………9分
(3)问题等价于证明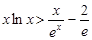 ,
, ,
,
由(1)可知 ,
, 的最小值为
的最小值为 ,当且仅当x=
,当且仅当x= 时取得
时取得
设 ,
, ,则
,则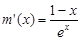 ,易得
,易得
 。当且仅当x=1时取得.从而对一切
。当且仅当x=1时取得.从而对一切 ,都有
,都有 成立
成立
| 6 |
| 5 |
| C1E |
| C1F |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com