
题目列表(包括答案和解析)
如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,且
为正方形,且![]() 平面
平面![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
(Ⅰ)证明:EF∥平面PCD;
(Ⅱ)求二面角B-CE-F的大小.
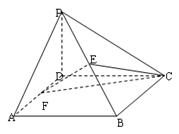
如图,在四棱锥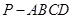 中,底面
中,底面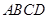 为正方形,侧棱
为正方形,侧棱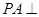 底面
底面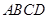 ,
,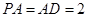 ,点
,点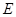 为
为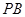 的中点。
的中点。
(Ⅰ)求证: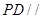 平面
平面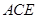 ;
;
(Ⅱ)求点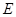 到平面
到平面 的距离。
的距离。

如图,在四棱锥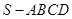 中,底面
中,底面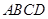 为正方形,侧棱
为正方形,侧棱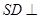 底面
底面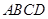 ,
,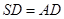 ,
,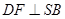 垂足为
垂足为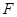 ,
,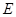 是
是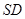 的中点.
的中点.
(Ⅰ)证明: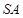 ∥平面
∥平面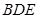 ;
;
(Ⅱ)证明:平面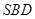 ⊥平面
⊥平面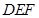 .
.
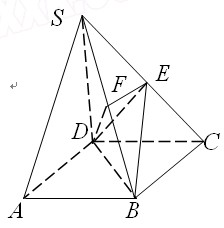
如图,在四棱锥 中,底面
中,底面 为正方形,
为正方形,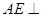 平面
平面 ,已知
,已知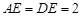 ,
,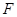 为线段
为线段 的中点.
的中点.
(1)求证: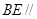 平面
平面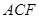 ;
;
(2)求四棱锥 的体积.
的体积.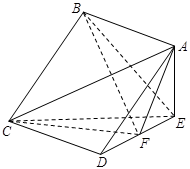
如图,在四棱锥 中,底面
中,底面 为正方形,
为正方形, 平面
平面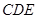 ,已知
,已知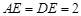 ,
, 为线段
为线段 的中点.
的中点.
(1)求证: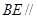 平面
平面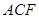 ;
;
(2)求二面角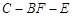 的平面角的余弦值.
的平面角的余弦值.
一、选择题
|