
题目列表(包括答案和解析)
设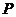 是半径为
是半径为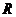 的圆周上一个定点,其中
的圆周上一个定点,其中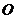 为圆心,连接
为圆心,连接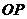 ,在圆周上等可能地任取一点
,在圆周上等可能地任取一点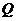 ,连接
,连接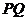 ,则弦
,则弦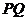 的长超过
的长超过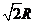 的概率为_________.
的概率为_________.
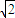 R的概率为( )
R的概率为( )


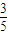
一、填空题:本大题共14小题,每小题5分,计70分.
1. 2.
2. 3.
3. 4.25
5.
4.25
5. 6.
6.
7. 8.③
9.6
10.50%(填0.5,
8.③
9.6
10.50%(填0.5, 都算对)
都算对)
11. 12.<
13.12
14.
12.<
13.12
14. 或
或
二、解答题:本大题共6小题,计90分.
15.解:(Ⅰ)当 时,点P共有28个,而满足
时,点P共有28个,而满足 的点P有19个,
的点P有19个,
从而所求的概率为 ………………………………………………………………………(7分)
………………………………………………………………………(7分)
(Ⅱ)当 时,由
时,由 构成的矩形的面积为
构成的矩形的面积为 ,而满足
,而满足
的区域的面积为 ,故所求的概率为
,故所求的概率为 ……………………………………(14分)
……………………………………(14分)
16.证:(Ⅰ)连接 交
交 于
于 ,连接
,连接 .
.
∵ 分别是
分别是 的中点,∴
的中点,∴ ∥
∥ 且
且 =
= ,∴四边形
,∴四边形 是矩形.
是矩形.
∴ 是
是 的中点………………………………………………………………………………(3分)
的中点………………………………………………………………………………(3分)
又∵ 是
是 的中点,∴
的中点,∴ ∥
∥ ……………………………………………………………(5分)
……………………………………………………………(5分)
则由 ,
, ,得
,得 ∥
∥ ………………………………………(7分)
………………………………………(7分)
(注:利用面面平行来证明的,类似给分)
(Ⅱ) ∵在直三棱柱 中,
中, ⊥底面
⊥底面 ,∴
,∴ ⊥
⊥ .
.
又∵ ,即
,即 ⊥
⊥ ,∴
,∴ ⊥面
⊥面 ………………………(9分)
………………………(9分)
而 面
面 ,∴
,∴ ⊥
⊥ ……………………………………………………………(12分)
……………………………………………………………(12分)
又 ,∴
,∴ 平面
平面 ……………………………………………………………(14分)
……………………………………………………………(14分)
17. 解:(Ⅰ)由 ,得
,得
 ,所以
,所以 ………………………………………………(4分)
………………………………………………(4分)
则 ,所以
,所以 ……………………………………………………(7分)
……………………………………………………(7分)
(Ⅱ)方案一:选择①③.
∵A=30°,a=1, +1)b=0,所以
+1)b=0,所以 ,则根据余弦定理,
,则根据余弦定理,
得 ,解得b=
,解得b= ,则c=
,则c= …………………(11分)
…………………(11分)
∴ …………………………………(14分)
…………………………………(14分)
方案二:选择②③. 可转化为选择①③解决,类似给分.
(注:选择①②不能确定三角形)
18. 解:(Ⅰ) ,即
,即 ,
,
 ,准线
,准线 ,
, ……………………………………………………(2分)
……………………………………………………(2分)
设⊙C的方程为 ,将O、F、A三点坐标代入得:
,将O、F、A三点坐标代入得:
 ,解得
,解得 ………………………………………………………(4分)
………………………………………………………(4分)
∴⊙C的方程为 ……………………………………………………(5分)
……………………………………………………(5分)
(Ⅱ)设点B坐标为 ,则
,则 ,整理得:
,整理得:
 对任意实数
对任意实数 都成立……………………………………………(7分)
都成立……………………………………………(7分)
∴ ,解得
,解得 或
或 ,
,
故当 变化时,⊙C经过除原点O外的另外一个定点B
变化时,⊙C经过除原点O外的另外一个定点B ……………………………(10分)
……………………………(10分)
(Ⅲ)由B 、
、 、
、 得
得 ,
,
∴ ,解得
,解得 ……………………………………………(12分)
……………………………………………(12分)
又 ,∴
,∴ ………………………………………………………………(14分)
………………………………………………………………(14分)
又椭圆的离心率 (
( )……………………(15分)
)……………………(15分)
∴椭圆的离心率的范围是 ………………………………………………………(16分)
………………………………………………………(16分)
19. (Ⅰ)证:因为对任意正整数 ,
, 总成立,
总成立,
令 ,得
,得 ,则
,则 …………………………………………(1分)
…………………………………………(1分)
令 ,得
,得 (1) , 从而
(1) , 从而 (2),
(2),
(2)-(1)得 ,
, …………………………………………………………………(3分)
…………………………………………………………………(3分)
综上得
 ,所以数列
,所以数列 是等比数列…………………………………………(4分)
是等比数列…………………………………………(4分)
(Ⅱ)正整数 成等差数列,则
成等差数列,则 ,所以
,所以 ,
,
则 ……………………………………………………(7分)
……………………………………………………(7分)
①当 时,
时, ………………………………………………………………(8分)
………………………………………………………………(8分)
②当 时,
时, …………………………(9分)
…………………………(9分)
③当 时,
时, ……………………(10分)
……………………(10分)
(Ⅲ)正整数 成等比数列,则
成等比数列,则 ,则
,则 ,
,
所以 ,
, ……………(13分)
……………(13分)
①当 ,即
,即 时,
时,
 ……………………………………………(14分)
……………………………………………(14分)
②当 ,即
,即 时,
时,
 ………………………………(15分)
………………………………(15分)
③当 ,即
,即 时,
时,
 ………………………………(16分)
………………………………(16分)
20. 解:
(Ⅰ)当 时,
时, .
.
因为当 时,
时, ,
, ,
,
且 ,
,
所以当 时,
时, ,且
,且 ……………………………………(3分)
……………………………………(3分)
由于 ,所以
,所以 ,又
,又 ,
,
故所求切线方程为 ,
,
即 …………………………………………………………………(5分)
…………………………………………………………………(5分)
(Ⅱ) 因为 ,所以
,所以 ,则
,则
当 时,因为
时,因为 ,
, ,
,
所以由 ,解得
,解得 ,
,
从而当 时,
时, ……………………………………………(6分)
……………………………………………(6分)
①
当 时,因为
时,因为 ,
, ,
,
所以由 ,解得
,解得 ,
,
从而当 时,
时, …………………………………………(7分)
…………………………………………(7分)
③当 时,因为
时,因为 ,
,
从而 一定不成立………………………………………………………………(8分)
一定不成立………………………………………………………………(8分)
综上得,当且仅当 时,
时, ,
,
故 …………………………………………(9分)
…………………………………………(9分)
从而当 时,
时, 取得最大值为
取得最大值为 …………………………………………………(10分)
…………………………………………………(10分)
(Ⅲ)“当 时,
时, ”等价于“
”等价于“ 对
对 恒成立”,
恒成立”,
即“ (*)对
(*)对 恒成立” ……………………………………(11分)
恒成立” ……………………………………(11分)
①
当 时,
时, ,则当
,则当 时,
时, ,则(*)可化为
,则(*)可化为
 ,即
,即 ,而当
,而当 时,
时, ,
,
所以 ,从而
,从而 适合题意………………………………………………………………(12分)
适合题意………………………………………………………………(12分)
②
当 时,
时, .
.
⑴
当 时,(*)可化为
时,(*)可化为 ,即
,即 ,而
,而 ,
,
所以 ,此时要求
,此时要求
 …………………………………………………………(13分)
…………………………………………………………(13分)
⑵
当 时,(*)可化为
时,(*)可化为 ,
,
所以 ,此时只要求
,此时只要求 ………………………………………………………(14分)
………………………………………………………(14分)
(3)当 时,(*)可化为
时,(*)可化为 ,即
,即 ,而
,而 ,
,
所以 ,此时要求
,此时要求 …………………………………………………………(15分)
…………………………………………………………(15分)
由⑴⑵⑶,得 符合题意要求.
符合题意要求.
综合①②知,满足题意的 存在,且
存在,且 的取值范围是
的取值范围是 ………………………………(16分)
………………………………(16分)
数学附加题部分
21.A.解:因为PA与圆相切于点A,所以 .而M为PA的中点,
.而M为PA的中点,
所以PM=MA,则 .
.
又 ,所以
,所以 ,所以
,所以 ……………………(5分)
……………………(5分)
在 中,由
中,由 ,
,
即 ,所以
,所以 ,
,
从而 ……………………………………………………………………………(10分)
……………………………………………………………………………(10分)
B.解: ,所以
,所以 =
= ……………………………(5分)
……………………………(5分)
即在矩阵 的变换下有如下过程,
的变换下有如下过程, ,
,
则 ,即曲线
,即曲线 在矩阵
在矩阵 的变换下的解析式为
的变换下的解析式为 ……(10分)
……(10分)
C.解:由题设知,圆心 ,故所求切线的直角坐标方程
,故所求切线的直角坐标方程
为 ……………………………………………………………………………(6分)
……………………………………………………………………………(6分)
从而所求切线的极坐标方程为 ………………………………(10分)
………………………………(10分)
D.证:因为 ,利用柯西不等式,得
,利用柯西不等式,得 …………………………(8分)
…………………………(8分)
即 ………………………………………………………………………(10分)
………………………………………………………………………(10分)
22.解: (Ⅰ)以A为原点,AB、AC、AP分别为x轴、y轴、z轴建立空间直角坐标系A-xyz,
则A(0,0,0),B(2,0,0),C(0,2,0),E(0,1,0),P(0,0,1),
所以 ,
, ……………………………(4分)
……………………………(4分)
故异面直线BE与PC所成角的余弦值为 ……………………………………(5分)
……………………………………(5分)
(Ⅱ)作PM⊥BE交BE(或延长线)于M,作CN⊥BE交BE(或延长线)于N,
则存在实数m、n,使得 ,
, 即
即
因为 ,所以
,所以
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com