
题目列表(包括答案和解析)
动点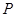 到两定点
到两定点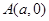 ,
,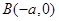 连线的斜率的乘积为
连线的斜率的乘积为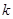 (
(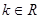 ),则动点P在以下哪些曲线上( )(写出所有可能的序号)
),则动点P在以下哪些曲线上( )(写出所有可能的序号)
① 直线 ② 椭圆 ③ 双曲线 ④ 抛物线 ⑤ 圆
A.①⑤ B.③④⑤ C.①②③⑤ D.①②③④⑤
动点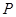 到两定点
到两定点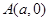 ,
,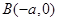 连线的斜率的乘积为
连线的斜率的乘积为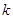 (
(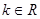 ),则动点P在以下哪些曲线上( )(写出所有可能的序号)
),则动点P在以下哪些曲线上( )(写出所有可能的序号)
① 直线 ② 椭圆 ③ 双曲线 ④ 抛物线 ⑤ 圆
| A.①⑤ | B.③④⑤ | C.①②③⑤ | D.①②③④⑤ |
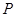 到两定点
到两定点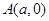 ,
,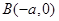 连线的斜率的乘积为
连线的斜率的乘积为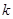 (
(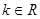 ),则动点P在以下哪些曲线上( )(写出所有可能的序号)
),则动点P在以下哪些曲线上( )(写出所有可能的序号)| A.①⑤ | B.③④⑤ | C.①②③⑤ | D.①②③④⑤ |
.动点 到两定点
到两定点 ,
, 连线的斜率的乘积为
连线的斜率的乘积为 (
( ),则动点P在以下哪些曲线上( )(写出所有可能的序号)
),则动点P在以下哪些曲线上( )(写出所有可能的序号)
① 直线 ② 椭圆 ③ 双曲线 ④ 抛物线 ⑤ 圆
A.①⑤ B.③④⑤ C.①②③⑤ D.①②③④⑤
1―5、 CDDCA 6―10、DABAB 11、 12、1, 9
12、1, 9
13解:因为方程x 2 + mx + 1=0有两个不相等的实根,
所以Δ1=m 2 ? 4>0, ∴m>2或m < ? 2
又因为不等式4x 2 +4(m ? 2)x + 1>0的解集为R,
所以Δ2=16(m ? 2) 2? 16<0, ∴1< m <3
因为p或q为真,p且q为假,所以p与q为一真一假,
(1)当p为真q为假时,
(2)当p为假q为真时,
综上所述得:m的取值范围是 或
或
14、解:
直线方程为y=-x+4,联立方程 ,消去y得,
,消去y得, .
.
设A( ),B(
),B( ),得
),得
所以: ,
,
由已知 可得
可得 +
+ =0,从而16-8p=0,得p=2.
=0,从而16-8p=0,得p=2.
所以抛物线方程为y2=4x,焦点坐标为F(1,0)
15、解(Ⅰ) AC与PB所成角的余弦值为 .
.
(Ⅱ)N点到AB、AP的距离分别为1, .
.
16解: (1) ; (2)略
; (2)略
17、6 18、①②③⑤ 19、B 20、B
21、解:(1)略 (2)
22、解:(1)设双曲线C的渐近线方程为y=kx,则kx-y=0
∵该直线与圆 相切,∴双曲线C的两条渐近线方程为y=±x.
相切,∴双曲线C的两条渐近线方程为y=±x.
故设双曲线C的方程为 .又双曲线C的一个焦点为
.又双曲线C的一个焦点为 ,
,
∴ ,
, ∴双曲线C的方程为:
∴双曲线C的方程为: .
.
(2)由 得
得 .令
.令
∵直线与双曲线左支交于两点,等价于方程f(x)=0在 上有两个
上有两个
不等负实根.
因此 ,解得
,解得 ..
..
(3). ∵ AB中点为 ,
,
∴直线l的方程为: .
令x=0,得
.
令x=0,得 .
.
∵ ,∴
,∴ ,∴
,∴ .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com