20080522
二、填空题：
13．13 14． 
15． 
16．②③
三、解答题：
17．解:(1) f(
)=sin(2－)+1－cos2(－)
= 2[sin2(－)－ cos2(－)]+1
=2sin[2(－)－]+1
= 2sin(2x－) +1 …………………………………………5分
∴ T==π…………………………………………7分
(2)当f(x)取最大值时， sin(2x－)=1，有 2x－ =2kπ+ ……………10分
即=kπ+
(k
Z) …………………………………………11分
∴所求的集合为{x∈R|x= kπ+
， (kZ)}．…………………………12分
18．解：(1) ：当
时，
,…………………………………………1分
当
时,
.
……………………………………………………………………………………3分
是等差数列,
, 
??????????…………………………………………5?分
(2)解：
, 
.…………………………………………7分
又
,
,
……………………………………8分
??????????…………………………………………??9分
又
得
.
,
,即
是等比数列. ………………………11分
所以数列的前
项和
.………………………12分
19．解（1）∵函数
的图象的对称轴为
要使在区间
上为增函数，
当且仅当
>0且
……………………2分
若=1则
=－1，
若=2则=－1，1
若=3则=－1，1，；………………4分
∴事件包含基本事件的个数是1+2+2=5
∴所求事件的概率为
………………6分
（2）由（1）知当且仅当
且>0时，
函数
上为增函数，
依条件可知试验的全部结果所构成的区域为
构成所求事件的区域为三角形部分。………………8分
由
………………10分
∴所求事件的概率为
………………12分
20解：(1):作
面
于
,连
取
的中点
,连
、
,
则有
……………………………4分
…………………………6分
(2)设
为所求的点,作
于
,连
.则
∥
………7分
就是
与面所成的角,则
.……8分
设
,易得
……………………………………10分
解得
………11分
故线段
上存在点,且
时,与面成
角. …………12分
21．解（1）由
得
∵
过点（2，
）的直线方程为
，即
（2）由
令
在其定义域（0，+
）上单调递增。
只需
恒成立
①由
上恒成立
∵
，∴
，∴
，∴
…………………………10分
综上k的取值范围为
………………12分
22．解：（1）由题意椭圆的离心率
∴
∴
∴
∴椭圆方程为
………………3分
又点（1，
）在椭圆上，∴
∴
=1
∴椭圆的方程为
………………6分
（2）若直线
斜率不存在，显然
不合题意；
则直线l的斜率存在。……………………7分
设直线为
，直线l和椭交于
，
。
将
依题意：
………………………………9分
由韦达定理可知：
………………10分
又
而
从而
………………13分
求得
符合
故所求直线MN的方程为：
………………14分
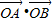为定值；
为定值；