
题目列表(包括答案和解析)
 如图15所示,质量为 m、电量为+q的带电小球固定于一不可伸长的绝缘细线一端,绳的另一端固定于O点,绳长为
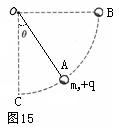
如图15所示,质量为 m、电量为+q的带电小球固定于一不可伸长的绝缘细线一端,绳的另一端固定于O点,绳长为![]() ,O点有一电荷量为+Q(Q>>q)的点电荷P,现加一个水平和右的匀强电场,小球静止于与竖直方向成 θ=300角的A点。求:
,O点有一电荷量为+Q(Q>>q)的点电荷P,现加一个水平和右的匀强电场,小球静止于与竖直方向成 θ=300角的A点。求:
(1)小球静止在A点处绳子受到的拉力;
(2) 外加电场大小;
(3)将小球拉起至与O点等高的B点后无初速释放,则小球经过最低点C时,绳受到的拉力
如图15所示,质量为 m、电量为+q的带电小球固定于一不可伸长的绝缘细线一端,绳的另一端固定于O点,绳长为![]() ,O点有一电荷量为+Q(Q>>q)的点电荷P,现加一个水平向右的匀强电场,小球静止于与竖直方向成 θ=300角的A点。求:
,O点有一电荷量为+Q(Q>>q)的点电荷P,现加一个水平向右的匀强电场,小球静止于与竖直方向成 θ=300角的A点。求:
(1)小球静止在A点处绳子受到的拉力和外加电场大小;
(2)将小球拉起至与O点等高的B点后无初速释放,则小球经过最低点C时,绳受到的拉力。

 ,O点有一电荷量为+Q(Q>>q)的点电荷P,现加一个水平向右的匀强电场,小球静止于与竖直方向成 θ=300角的A点。求:
,O点有一电荷量为+Q(Q>>q)的点电荷P,现加一个水平向右的匀强电场,小球静止于与竖直方向成 θ=300角的A点。求:
如图15所示,PQ、MN两极板间存在匀强电场,两极板间电势差为U、间距为d,MN极板右侧虚线区域内有垂直纸面向内的匀强磁场。现有一初速度为零、带电量为q、质量为m的离子从PQ极板出发,经电场加速后,从MN上的小孔A垂直进入磁场区域,并从C点垂直于虚线边界射出。求:
(1)离子从小孔A射出时速度v0;
(2)离子带正电还是负电?C点离MN板的距离?

(18分)
如图15所示,PQ、MN两极板间存在匀强电场,两极板间电势差为U、间距为d,MN极板右侧虚线区域内有垂直纸面向内的匀强磁场。现有一初速度为零、带电量为q、质量为m的离子从PQ极板出发,经电场加速后,从MN上的小孔A垂直进入磁场区域,并从C点垂直于虚线边界射出。求:
(1)离子从小孔A射出时速度v0;
(2)离子带正电还是负电?C点离MN板的距离?
1、C 2、D 3、A 4、A 5、B 6、BD 7、ACD 8、AC 9、AB
10、(12分)①5.50;②2.75,1.10;
③ ;④滑块的质量m;
;④滑块的质量m; 
11、(8分)①.D
②  ,θ是n个点对应的圆心角,t是电火花计时器的打点时间间隔;
,θ是n个点对应的圆心角,t是电火花计时器的打点时间间隔;
③.没有影响 ,电火花计时器向卡纸中心移动时不影响角度的测量
12、(12分)解:(1)带电粒子A处于平衡,其受力如图,其中F为两点电荷间的库仑力,T为绳子拉力,E0为外加电场,则
 Tcosθ-mg-Fcosθs=0 1…………………………(2分)
Tcosθ-mg-Fcosθs=0 1…………………………(2分)
Fsinθ+qE0-Tsinθ=0 2……………………………(2分)
 3……………………………(2分)
3……………………………(2分)
联立式解得:有
 4……………………………(2分)
4……………………………(2分)
 5…………………………………(2分)
5…………………………………(2分)
(2)小球从B运动到C的过程中,q与Q间的库仑力不做功,由动能定理得
 6………………………………………………………(2分)
6………………………………………………………(2分)
在C点时:  7……………………………………(2分)
7……………………………………(2分)
联立5、6、7解得:  8……………(2分)
8……………(2分)
13(12分).解:设中央恒星质量为M,A行星质量为m,则由万有引力定律和牛顿第二定律得  ①
①
解得  ②
②
(2)由题意可知,A、B相距最近时,B对A的影响最大,且每隔t0时间相距最近。
设B行星周期为TB,则有: ③
③
解得: ④
④
设B行星的质量为mB,运动的轨道半径为RB,则有
 ⑤
⑤
由①④⑤得: ⑥
⑥
14、(14分)(1)设轨道半径为R,由机械能守恒定律: (1)(2分)
(1)(2分)
对B点: (2)
(2) (2分)
(2分)
对A点: (3)(2分)
(3)(2分)
由(1)、(2)、(3)式得:两点的压力差: -(4)
-(4)
由图象得:截距
 ,得
,得 (5)(2分)
(5)(2分)
(2)因为图线的斜率
所以 (6)(2分)
(6)(2分)
在A点不脱离的条件为:
 (7)(2分)
(7)(2分)
由(1)、(6)、(7)式得: (8)(2分)
(8)(2分)
23.(15分)(1)由 eU=mv02(1分) 得电子进入偏转电场区域的初速度v0=(1分)
设电子从MN离开,则电子从A点进入到离开匀强电场区域的时间t= =d (1分);
y=at2=(2分)
因为加速电场的电势差U>, 说明y<h,说明以上假设正确(1分)
所以vy=at=´ d = (1分)
离开时的速度v==(2分)
(2)设电子离开电场后经过时间t’到达x轴,在x轴方向上的位移为x’,则
x’=v0t’(1分),y’=h-y=h-t=vyt’ (1分)
则 l=d+x’= d+v0t’= d+v0(-)= d+h-=+h(1分)
代入解得 l=+(2分)
16、(16分)(1)根据牛顿第二定律,滑块相对车滑动时的加速度
 (1分)
(1分)
滑块相对车滑动的时间  (1分)
(1分)
滑块相对车滑动的距离  (1分)
(1分)
滑块与车摩擦产生的内能  (1分)
(1分)
由上述各式解得  (与动摩擦因数μ无关的定值) (1分)
(与动摩擦因数μ无关的定值) (1分)
(2)设恒力F取最小值为F1,滑块加速度为a1,此时滑块恰好到达车的左端,则
滑块运动到车左端的时间  ①
①
由几何关系有  ② (1分)
② (1分)
由牛顿定律有  ③ (1分)
③ (1分)
由①②③式代入数据解得  ,
, (2分)
(2分)
则恒力F大小应该满足条件是  (1分)
(1分)
(3)力F取最小值,当滑块运动到车左端后,为使滑块恰不从右端滑出,相对车先做匀加速运动(设运动加速度为a2,时间为t2),再做匀减速运动(设运动加速度大小为a3).到达车右端时,与车达共同速度.则有
 ④ (1分)
④ (1分)
 ⑤ (1分)
⑤ (1分)
 ⑥ (1分)
⑥ (1分)
由④⑤⑥式代入数据解得  (1分)
(1分)
则力F的作用时间t应满足  ,即
,即 (2分)
(2分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com