
题目列表(包括答案和解析)

 (2009•台州二模)如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为B点,且AB=AC=A1B=2.
(2009•台州二模)如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为B点,且AB=AC=A1B=2.| 14 |
 如图是一个方形迷宫,甲、乙两人分别位于迷宫的A、B两处,两人同时以每一分钟一格的速度向东、西、南、北四个方向行走,已知甲向东、西行走的概率都为
如图是一个方形迷宫,甲、乙两人分别位于迷宫的A、B两处,两人同时以每一分钟一格的速度向东、西、南、北四个方向行走,已知甲向东、西行走的概率都为| 1 |
| 4 |
| 1 |
| 3 |
如图是一个方形迷宫,甲、乙两人分别位于迷宫的 两处,两人同时以每一分钟一格的速度向东、西、南、北四个方向行走,已知甲向东、西行走的概率都为
两处,两人同时以每一分钟一格的速度向东、西、南、北四个方向行走,已知甲向东、西行走的概率都为 ,向南、北行走的概率为
,向南、北行走的概率为 和
和 ,乙向东、西、南、北四个方向行走的概率均为
,乙向东、西、南、北四个方向行走的概率均为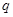
⑴求 和
和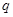 的值;
的值;
⑵问最少几分钟,甲、乙二人相遇?并求出最短时间内可以相遇的概率。

(1)方程有两个正根的充要条件;
(2)方程至少有一个正根的充要条件.?
思路分析:先求出方程有两个实根的充要条件,再讨论x2的系数及运用根与系数的关系分别求出要求的充要条件.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com