
题目列表(包括答案和解析)
(09年济宁一中反馈一)(14分)已知函数![]() 的导数
的导数![]() 满足:①
满足:①![]() ;②对一切实数
;②对一切实数![]() ,不等式
,不等式![]() 恒成立。
恒成立。
(1)求![]()
(2)求![]() 的解析式。
的解析式。
已知直线 为曲线
为曲线 在点
在点 处的切线,直线
处的切线,直线 是该曲线的另一条切线,且
是该曲线的另一条切线,且 。
。
(1)求直线 和
和 的方程。
的方程。
(2)求直线 、
、 与x轴围成的三角形的面积。
与x轴围成的三角形的面积。
【解析】本试题主要考查了导数的几何意义的运用,求解切线方程以及运用三角形的面积公式的综合运用试题。
已知直线 为曲线
为曲线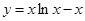 在点
在点 处的切线,直线
处的切线,直线 是该曲线的另一条切线,且
是该曲线的另一条切线,且 。
。
(1)求直线 和
和 的方程。
的方程。
(2)求直线 、
、 与x轴围成的三角形的面积。
与x轴围成的三角形的面积。
【解析】本试题主要考查了导数的几何意义的运用,求解切线方程以及运用三角形的面积公式的综合运用试题。
| 1 | 2 |
 14、如图是y=f(x)导数的图象,对于下列四个判断:
14、如图是y=f(x)导数的图象,对于下列四个判断:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com