练习册

  • 练习册
  • 试题
    Hippasus虽然死了.但他的“无公度比 的观念并没有随之消亡.Plato学派的前驱Theodorus又证明了..也没有公度比.可惜这一学派又不愿接受无理数这一新概念.之后的Eudoxus及Euclid是通过“量 概念的引入.用几何方法处理这种“无公度比 (用现在的话说.就是找近似的有理数来代替这个数).这又基本上将无理数抹杀.在东方的印度.也同样在十二世纪仍将无理数当作有理数加以处理.直至十九世纪的1872年.德国的Dedekind才将之分离出来.为区分以往的数而命名为无理数.将原有的可以化为整数比的数称有理数.并将无理数与有理数统称实数.创建了实数理论,之后的1874年.德国的Cator验证了Dedekind理论的正确性.并证明了“实数与数轴上点一一对应 的理论.至此.完成了真正意义上的实数理论.四.无聊游戏中出现的复数 【查看更多】

     

    题目列表(包括答案和解析)

    一医生知道某种疾病患者的自然痊愈率为，为实验一种新药是否有效，把它给10个病人服用．他事先决定，若这10个病人中至少有4个治好，则认为这种药有效，提高了痊愈率．否则认为无效．求

    （1）虽然新药有效，并把痊愈率提高到了，但通过实验却被否定的概率；

    （2）新药完全无效，但通过实验却被判断为有效的概率．

    参考数据：

    p

    2.0000

    3.0000

    4.0000

    5.0000

    6.0000

    7.0000

    8.0000

    9.0000

    10.0000

    0.2500

    0.0625

    0.0156

    0.0039

    0.0010

    0.0002

    0.0001

    0.0000

    0.0000

    0.0000

    0.3500

    0.1225

    0.0429

    0.0150

    0.0053

    0.0018

    0.0006

    0.0002

    0.0001

    0.0000

    0.6500

    0.4225

    0.2746

    0.1785

    0.1160

    0.0754

    0.0490

    0.0319

    0.0207

    0.0135

    0.7500

    0.5625

    0.4219

    0.3164

    0.2373

    0.1780

    0.1335

    0.1001

    0.0751

    0.0563

    答案请保留四位有效数字．

     

    查看答案和解析>>

    某市出租车的计价标准是：3km以内（含3km）10元；超出3km但不超过18km的部分1元km；超出18km的部分2元km．
    （1）如果某人乘车行驶了20km，他要付多少车费？某人乘车行驶了x km，他要付多少车费？
    （2）如果某人付了22元的车费，他乘车坐了多远？某人付了10+x（x＞0）元的车费，他乘车坐了多远？

    查看答案和解析>>

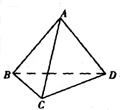    精英家教网数学课上，张老师用六根长度均为a的塑料棒搭成了一个正三棱锥（如图所示），然后他将其中的两根换成长度分别为在
    		2
    a    和
    		3
    a    的塑料棒、又搭成了一个三棱锥，陈成同学边听课边动手操作，也将其中的两根换掉，但没有成功，不能搭成三棱锥，如果两人都将BD换成了长为
    		3
    a    的塑料棒．
    （1）试问张老师换掉的另一根塑料棒是什么，而陈成同学换掉的另一根塑料棒又是什么？请你用学到的数学知识解释陈成同学失败的原因；
    （2）试证：平面ABD⊥平面CBD；
    （3）求新三棱锥的外接球的表面积．

    查看答案和解析>>

    迄今为止，人类已借助“网络计算”技术找到了630万位的最大质数，小胡发现由8个质数组成的数列41，43，47，53，61，71，83，97的一个通项公式，并根据通项公式得出数列的后几项，发现它们也是质数．小胡欣喜万分，但小胡按得出的通项公式，在往后写出几个数发现它不是质数．他写出不是质数的一个数是（　　）

    查看答案和解析>>

    （2013•成都二模）如图，某中学甲、乙两班共有25名学生报名参加了一项 测试．这25位学生的考分编成的茎叶图，其中 有一个数据因电脑操作员不小心删掉了（这里暂用x来表示），但他清楚地记得两班学生成绩的中位数相同．
    （I）求这两个班学生成绩的中位数及x的值；
    （II）如果将这些成绩分为“优秀”（得分在175分 以上，包括175分）和“过关”，若学校再从这两个班获得“优秀”成绩的考生中选出3名代表学校参加比赛，求这 3人中甲班至多有一人入选的概率．

    查看答案和解析>>


    同步练习册答案