
题目列表(包括答案和解析)
某种商品的成本为5元/件,开始按8元/件销售,销售量为50件,为了获取最大利润,商家先后采取了提价与降价两种措施进行试销。经试销发现:销售价每上涨1元每天销售量就减少10件;而降价后,日销售量Q (件)与实际销售价x (元)满足关系
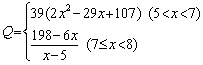
(1)求总利润(利润=销售额-成本) y
(元)与实际销售价x (件)的函数关
系式;
(2)试问:当实际销售价为多少元时,总利润最大.
某商家经亚组委授权销售广州亚运吉祥物“乐羊羊”小饰品,该饰品的成本是5元/件,开始按8元/件销售,日销售量为50件,为了获取最大利润,商家先后采取了提价与降价两种措施进行试销。经试销发现:销售价每上涨1元,每天销售量就减少10件;而降价后,日销售量Q(件)与实际销售价x(元)满足关系:
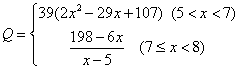
(Ⅰ)求商家经销该饰品每天的总利润y(元)与实际销售价x(元)的函数关系式;
(注:利润=销售额-成本)
(Ⅱ)试问:当实际销售价为多少元时,商家每天的总利润最大.
(本小题满分14分)某种商品的成本为5元/ 件,开始按8元/件销售,销售量为50件,为了获得最大利润,商家先后采取了提价与降价两种措施进行试销。经试销发现:销售价每上涨1元每天销售量就减少10件;而降价后,日销售量Q(件)与实际销售价x(元)满足关系:
|
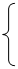
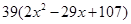
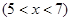 [
[
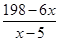
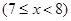 [
[
(1)求总利润(利润=销售额-成本)y(元)与销售价x(件)的函数关系式;
(2)试问:当实际销售价为多少元时,总利润最大.
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
C
B
B
C
D
C
A
C
D
A
二、填空题:
13.  14.
14.  15. 2个 16.
15. 2个 16. 

三、解答题:
17.解:(1)
 ……………………3分
……………………3分
又 
 即
即 

 …………………5分
…………………5分
(2)

又 
 是
是 的充分条件
的充分条件  解得
解得  ………12分
………12分
18.由题意知,在甲盒中放一球概率为 时,在乙盒中放一球的概率为
时,在乙盒中放一球的概率为 …2分
…2分
①当 时,
时, ,
, 的概率为
的概率为 ………4分
………4分
②当 时,
时, ,又
,又 ,所以
,所以 的可能取值为0,2,4
的可能取值为0,2,4
(?)当 时,有
时,有 ,
, ,它的概率为
,它的概率为 ………6分
………6分
(?)当 时,有
时,有 ,
, 或
或 ,
,
它的概率为
(?)当 时,有
时,有 或
或
它的概率为
故 的分布列为
的分布列为

0
2
4
P



 的数学期望
的数学期望 …………12分
…………12分
19.解:(1) 连接 交
交 于点E,连接DE,
于点E,连接DE, ,
,
 四边形
四边形 为矩形,
为矩形, 点E为
点E为 的中点,
的中点,



 平面
平面 ……………6分
……………6分
(2)作 于F,连接EF
于F,连接EF
 ,D为AB中点,
,D为AB中点, ,
,

 ,
,  EF为BE在平面
EF为BE在平面 内的射影
内的射影
又 为二面角
为二面角 的平面角.
的平面角.
设


又 二面角
二面角 的余弦值
的余弦值 ………12分
………12分
20.(1)据题意的
 ………4分
………4分
 ………5分
………5分
(2)由(1)得:当 时,
时,

当 时,
时, ,
, 为增函数
为增函数
当 时,
时, 为减函数
为减函数
 当
当 时,
时, …………………………8分
…………………………8分
当 时,
时,
当 时,
时,
当 时,
时, …………………………10分
…………………………10分
综上知:当 时,总利润最大,最大值为195 ………………12分
时,总利润最大,最大值为195 ………………12分
21.解:(1)由椭圆定义可得 ,由
,由 可得
可得
 ,而
,而
解得  ……………………4分
……………………4分
(2)由 ,得
,得 ,
,

解得 或
或 (舍去)
(舍去)  此时
此时
当且仅当 时,
时, 得最小值
得最小值 ,
,
此时椭圆方程为 ………………………………………8分
………………………………………8分
(3)由 知点Q是AB的中点
知点Q是AB的中点
设A,B两点的坐标分别为 ,中点Q的坐标为
,中点Q的坐标为
则 ,两式相减得
,两式相减得

 AB的中点Q的轨迹为直线
AB的中点Q的轨迹为直线 ①
①
且在椭圆内的部分
又由 可知
可知 ,所以直线NQ的斜率为
,所以直线NQ的斜率为 ,
,
方程为 ②
②
①②两式联立可求得点Q的坐标为
 点Q必在椭圆内
点Q必在椭圆内  解得
解得
又
 …………………………………12分
…………………………………12分
22.解:(1)由 ,得
,得
令 ,有
,有


又


(2)证明:

 为递减数列
为递减数列
当 时,
时, 取最大值
取最大值

由(1)中知

综上可知
(3)
欲证: 即证
即证
即 ,构造函数
,构造函数
 当
当 时,
时,
 函数
函数 在
在 内递减
内递减
 在
在 内的最大值为
内的最大值为
 当
当 时,
时,
又

 不等式
不等式 成立
成立
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com