练习册

  • 练习册
  • 试题
    (1)求的最小正周期, 【查看更多】

     

    题目列表(包括答案和解析)



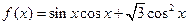
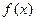    （Ⅰ）求的最小正周期；
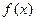    （Ⅱ）求在区间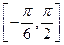上的最大值和最小值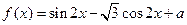

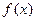    查看答案和解析>>



    (1)求的最小正周期和单调增区间；
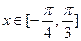    (2)当时，函数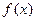的最大值与最小值的和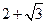，求

    查看答案和解析>>

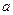
    已知．

        (Ⅰ)求的最小正周期；

        (Ⅱ)当为何值时，取得最大值，最大值是多少?

        (Ⅲ)求的单调递减区间.

    查看答案和解析>>

    最小正周期为π的函数(其中a是小于零的常数，是大于零的常数)的图象按向量，(0＜θ＜π)平移后得到函数y＝f(x)的图象，而函数y＝f(x)在实数集上的值域为[－2，2]，且在区间上是单调递减函数．

    (1)求a、和θ的值；

    (2)若角α和β的终边不共线，f(α)＋g(α)＝f(β)＋g(β)，求tan(α＋β)的值．

    查看答案和解析>>

    函数的最小正周期为,

    （Ⅰ）求的单调递增区间； 

    （Ⅱ）在中,角A,B,C的对边分别是,且满足,

    求角B的值，并求函数的取值范围.

    查看答案和解析>>

    一、选择题(5分×12=60分)   

        B  B  D  D  C  B  B  D  D  C  A  A

    二、填空题(4分x 4=16分)

      13．0.1  14．63  15．  16．①③

    三、解答题(12分×5+14分=74分)

    17．解：(1)2分

            ……………………4分

             ∴的最小正周期为 …………………6分(2)∵成等比数列   ∴

    ∴≥       ………………………8分

    ∵   ∴≤即 ≤

    ∵   ∴≤         ………………………………………………10分

    18．解：(1)设公差由成等比数列得 …………………1分

    ∴即 ∴舍去或     …………………………3分

    ∴           ………………………………………………4分

    又              ………………………………………………5分

    ∴

           ………………………………………7分

    (2)                ………………………………………………8分

    当时，  ………………………………………10分

    当时，   …………………………7分

    19．解：(1)记“任取2张卡片，将卡片上的函数相加得到偶函数”为事件A，

                    ……………………………………………………4分

    (2)可能值为        ……………………………………………………………5分

          …………………………10分

    ∴     …………………………12分

    20．解：(1)连结    为正△ …1分

                      

                                           面3分

    面面          

     

    即点的位置在线段的四等分点且靠近处  ………………………………………6分(2)过作于，连

    由(1)知面(三垂线定理)

    ∴为二面角的平面角……9分

       

       

    在中，

    在中，

    ∴二面角的大小为     ………………………………………12分

    (说明：若用空间向量解，请参照给分)

    21．解：(1)设，由取得

     

    则……………………2分

    ∴…………………………12分

    又∵为定值， 则        ………………5分

    ∵为定值，∴为定值。

    (2)∵，∴抛物线方程为：设点则

    由(1)知 则         ………………………………8分

    又∵过点  ∴  ∴  ∴………………………………9分

    代入椭圆方程得：

    ∴≥  ………………11分

                      

    当且仅当                 即           上式取等号

                        

    ∴此时椭圆的方程为：             ………………………………………12分

    22．解：(1)∵  ∴…1分

        设 则  ……2分

    ∴在上为减函数  又   

    时，，∴ ∴在上是减函数………4分(2)①∵ ∴或时

     ∴…………………………………6分

    又≤≤对一切恒成立 ∴≤≤        ……………8分

    ②显然当或时，不等式成立                 …………………………9分

    当，原不等式等价于≥ ………10分

    下面证明一个更强的不等式：≥…①

    即≥……②亦即≥ …………………………11分

    由(1) 知在上是减函数   又  ∴……12分

    ∴不等式②成立，从而①成立  又

    ∴＞

    综合上面∴≤≤且≤≤时，原不等式成立     ……………………………14分

     

     

     


    同步练习册答案