
题目列表(包括答案和解析)
如图,探索n×n的正方形钉子板上(n是钉子板每边上的钉子数),连接任意两个钉子所得到的不同长度值的线段种数:当n=2时,钉子板上所连不同线段的长度值只有1与 ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;那么当n=5时,
S=_________;对n×n的钉子板,写出用n表示S的代数式S=_____________________。
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;那么当n=5时,
S=_________;对n×n的钉子板,写出用n表示S的代数式S=_____________________。

n=2 n=3 n=4 n=5
第16题图
如图,已知反比例函数y= 过点P, P点的坐标为(3-m,2m),m是分式方程
过点P, P点的坐标为(3-m,2m),m是分式方程 的解,PA⊥x轴于点A,PB⊥y轴于点B.
的解,PA⊥x轴于点A,PB⊥y轴于点B.
(1)试判断四边形PAOB的形状,并说明理由.
(2)连结AB,E为AB上的一点,EF⊥BP于点F,G为AE的中点,连结OG、FG,试问FG和OG有何数量关系?请写出你的结论并证明.
(3)若M为反比例函数y= 在第三象限内的一动点,过M作MN⊥x轴于交AB的延长线于点N,是否存在一点M使得四边形OMNB为等腰梯形?若存在,请求出M点的坐标;若不存在,请说明理由.
在第三象限内的一动点,过M作MN⊥x轴于交AB的延长线于点N,是否存在一点M使得四边形OMNB为等腰梯形?若存在,请求出M点的坐标;若不存在,请说明理由.
下面是小明对多项式 进行因式分解的过程.
进行因式分解的过程.
解:设 .
.
原式= (第一步)
(第一步)
= (第二步)
(第二步)
= (第三步)
(第三步)
= (第四步)
(第四步)
回答下列问题:
(1)小明从第二步到第三步运用了因式分解的 .
| A.提取公因式 | B.平方差公式 |
| C.两数和的完全平方公式 | D.两数差的完全平方公式 |
 进行因式分解.
进行因式分解.探索规律:货物箱按如图方式堆放(自下而上依次为第1层、第2层、…),受堆放条件限制,堆放时应符合下列条件:每层堆放货物箱的个数 与层数n之间满足关系式
与层数n之间满足关系式 ,
, 为正整数.
为正整数. 
例如,当 时,
时,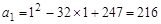 , 当
, 当 时,
时, ,则:
,则: = ,
= , = ;
= ;
⑵ 第n层比第(n+1)层多堆放 个货物箱.(用含n的代数式表示)
如图,已知反比例函数y= 过点P, P点的坐标为(3-m,2m),m是分式方程
过点P, P点的坐标为(3-m,2m),m是分式方程 的解,PA⊥x轴于点A,PB⊥y轴于点B.
的解,PA⊥x轴于点A,PB⊥y轴于点B.
(1)试判断四边形PAOB的形状,并说明理由.

(2)连结AB,E为AB上的一点,EF⊥BP于点F,G为AE的中点,连结OG、FG,试问FG和OG有何数量关系?请写出你的结论并证明.

(3)若M为反比例函数y= 在第三象限内的一动点,过M作MN⊥x轴于交AB的延长线于点N,是否存在一点M使得四边形OMNB为等腰梯形?若存在,请求出M点的坐标;若不存在,请说明理由.
在第三象限内的一动点,过M作MN⊥x轴于交AB的延长线于点N,是否存在一点M使得四边形OMNB为等腰梯形?若存在,请求出M点的坐标;若不存在,请说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com