
题目列表(包括答案和解析)
阅读材料:如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=900,且点D 在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD。
解决问题:
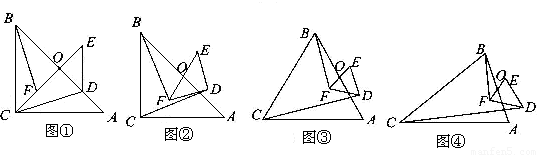
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中结论仍然成立吗?如果成立,请说明理由;如果不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为O,且顶角∠ACB=∠EDF=α,请直接写出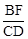 的值(用含α的式子表示出来)。
的值(用含α的式子表示出来)。
(本题12分)已知:如图,二次函数![]() 的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
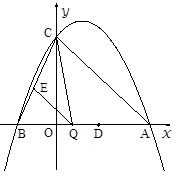
1.(1)求该二次函数的关系式;
2.(2)写出该二次函数的对称轴和顶点坐标;
3.(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
4.(4)若平行于x轴的动直线![]() 与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线
与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线![]() ,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
(本题12分)已知:如图,二次函数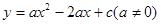 的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
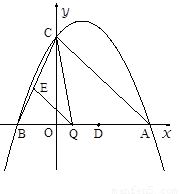
1.(1)求该二次函数的关系式;
2.(2)写出该二次函数的对称轴和顶点坐标;
3.(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
4.(4)若平行于x轴的动直线 与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线
与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线 ,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
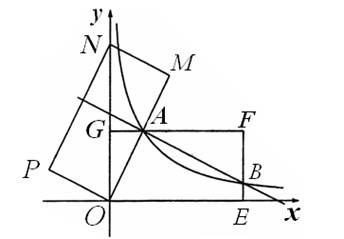
如图,在平面直角坐标系xOy中,矩形OEFG的顶点F坐标为(4,2),OG边与y轴重合。将矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,OM
与GF交于点A.
1.判断△OGA和△NPO是否相似,并说明理由;
2.求过点A的反比例函数解析式;
3.若(2)中求出的反比例函数的图象与EF交于B点,请探索:直线AB与OM的位置关系,并说明理由.
4.在GF所在直线上,是否存在一点Q,使△AOQ为等腰三角形.若存在,请直接写出
所有满足要求的Q点坐标.
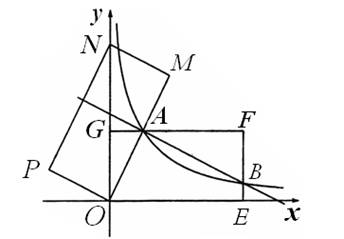
如图,在平面直角坐标系xOy中,矩形OEFG的顶点F坐标为(4,2),OG边与y轴重合。将矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,OM
与GF交于点A.
1.判断△OGA和△NPO是否相似,并说明理由;
2.求过点A的反比例函数解析式;
3.若(2)中求出的反比例函数的图象与EF交于B点, 请探索:直线AB与OM的位置关系,并说明理由.
4.在GF所在直线上,是否存在一点Q,使△AOQ为等腰三角形.若存在,请直接写出
所有满足要求的Q点坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com