
题目列表(包括答案和解析)
(本小题满分12分) 已知函数f(x)=2sin(x+![]() )cos(x+
)cos(x+![]() )+2
)+2![]() cos2(x+
cos2(x+![]() )-
)-![]() ,α为常数.(Ⅰ)求函数f(x)的周期; (Ⅱ)若0≤α≤π时,求使函数f(x)为偶函数的α值.
,α为常数.(Ⅰ)求函数f(x)的周期; (Ⅱ)若0≤α≤π时,求使函数f(x)为偶函数的α值.
(本小题满分12分)已知函数f(x)=ln(x+1)-x.
⑴求函数f(x)的单调递减区间;
⑵若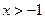 ,证明:
,证明: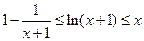 .
.
(本小题满分12分) 已知函数f(x)=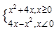 (1)作出函数
(1)作出函数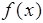 的图像简图,并指出函数
的图像简图,并指出函数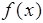 的单调区间;
(2)若f(2-a2)>f(a),求实数a的取值范围.
的单调区间;
(2)若f(2-a2)>f(a),求实数a的取值范围.
(本小题满分12分)
已知函数f(x)=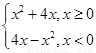
(1)作出函数 的图像简图,并指出函数
的图像简图,并指出函数 的单调区间;
的单调区间;
(2)若f(2-a2)>f(a),求实数a的取值范围.
(本小题满分12分)已知函数f(x)=x3+x2-2.
(1)设{an}是正数组成的数列,前n项和为Sn,其中a1=3.若点(an,an+12-2an+1)(n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(2)求函数f(x)在区间(a-1,a)内的极值.
1.A 2.B 3.C 4.D 5.C 6.A 7.B 8.C 9.B 10.A 11.C 12.D
13.270 14. 15. 16.
17.解:(1)a?b=cosx?cos-sinx?sin=cos 2x.2分
|a+b|===2.4分
又∵x∈[0,],∴cos x>0,∴|a+b|=2cos x.5分
(2)f(x)=cos 2x-4λcos x,
即f(x)=2(cos x-λ)2-1-2λ2.6分
①当0≤λ≤1时,当且仅当cos x=λ时,f(x)取得最小值-1-2λ2,
∴-1-2λ2=-,解得λ=.8分
②当λ>1时,当且仅当cos x=1时,f(x)取得最小值1-4λ,
∴1-4λ=-,解得λ=(舍).10分
③当λ<0时,当且仅当cos x=0时,f(x)取得最小值-1,无解.11分
综上所述,λ=为所求.12分
18.解:(1)设箱子内装着n个写有数字“
则=.2分
解得n=4.4分
∴该箱子内装有4个写有数字“08”的球.
(2)当游戏结束时,总取球数为1的概率是;6分
当游戏结束时,总取球数为2的概率是×=;8分
当游戏结束时,总取球数为3的概率是××=;10分
∴当游戏结束时,总取球数不多于3的概率是.12分
19.解:(1)延长CG交AB于N,∵G是△ABC的重心,∴N是AB的中点.1分
∵∠ACB=90°,∴CN=AB=6,∴CG=CN=4.2分
而DC⊥平面ABC,∴三角形DCG是等腰直角三角形,
即直线DG与平面ABC所成的角为45°.4分
(2)作ME∥GC交DC于E,∴∠EMB是异面直线GC与BM所成的角或补角.5分
∵M是DG的中点,ME=GC=2,
BE===2.6分
过M作MH⊥GC于H,MH⊥平面ABC,∴MH=2,
∴MB2=MH2+HB2=4+4+36-2?2?6?cos 60°=32,
∴cos∠EMB==-.7分
∴异面直线GC与BM所成的角为arccos.8分
(2)过B作直线BF⊥GC于F, BF⊥平面GMC.9分
∵△CNB是正三角形,故BF=BCcos 30°=3,过F作FS⊥MC于S,连BS,三角形DCG是等腰直角三角形.10分
M为GD的中点,∴GD⊥CM,
∴FS∥GD,FS=FCsin 45°=.11分
∴tan∠FSB==,
∴二面角B―MC―G的大小是arctan.12分
20.解:(1)由函数f(x)=-x4+x3+ax2-2x-2在区间[-1,1]上是单调递减,在区间[1,2]上单调递增,所以x=1取得极小值.1分
∴f′(1)=0,∴-1+2+
∴a=.4分
(2)由(1)知f(x)=-x4+x3+x2-2x-2,
∴f′(x)=-x3+2x2+x-2.5分
令f′(x)=0,得x=-1,x=1,x=2.6分
∴函数f(x)有极大值f(-1)=-,f(2)=-,极小值f(1)=-.8分
∵关于x的方程f(2x)=m有三个不同的实数解,令2x=t(t>0),
即关于t的方程f(t)=m在t∈(0,+∞)上有三个不同的实数解.9分
在t∈(0,+∞)上y=f(t)与y=f(x)图象一致.11分
又f(0)=-2,由数形结合可知,-<m<-.12分
21.解:(1)由An=(an-1),An+1=(an+1-1).1分
∴an+1=(an+1-an),即=3,2分
且a1=A1=(a1-1),
得a1=3.3分
∴数列{an}是以3为首项,3为公比的等比数列.4分
通项公式为an=3n.5分
(2)不妨设数列{dn}中的第n项分别是数列{an}的第p项和数列{bn}的第q项,即3p=4q+3.6分
所以(4-1)p=4q+3.7分
∴C4p+C4p-1(-1)1+…+C4?(-1)p-1+C(-1)p=4q+3.8分
4q=4k+(-1)p-3,(k∈Z,p,q∈Z*).9分
p为奇数,当p=1时,q=0(舍去).10分
∴p=2n+1,所以dn=a2n+1=32n+1.12分
22.解:(1)由|PF1|-|PF2|=2<|F
故轨迹S的方程为x2-=1(x≥1).4分
(2)当直线l的斜率存在时,设直线方程为y=k(x-2),P(x1,y1),Q(x2,y2)与双曲线方程联立消y得(k2-3)x2-4k2x+4k2+3=0.5分
∴解得k2>3.6分
∵?=(x1-m)(x2-m)+y1y2
=(x1-m)(x2-m)+k2(x1-2)(x2-2)
=(k2+1)x1x2-(2k2+m)(x1+x2)+m2+4k2
=+m2.7分
∵MP⊥MQ,∴?=0,
故得3(1-m2)+k2(m2-
∴解得m=-1.8分
当m=-1时,MP⊥MQ,当直线l的斜率不存在时,由P(2,3),Q(2,-3)及M(-1,0)知结论也成立.
综上,当m=-1时,MP⊥MQ.9分
(3)∵a=1,c=2,∴x=是双曲线的右准线.10分
由双曲线定义得:|PA|=|PF2|=|PF2|,|QB|=|QF2|.
(法一)∴λ==
===11分
∵k2>3,∴0<< ,故<λ<.12分
注意到直线的斜率不存在时,|PQ|=|AB|,此时,λ=.13分
综上,λ∈[,).14分
(法二)设直线PQ的倾斜角为θ,由于直线PQ与双曲线右支有二个交点,
∴<θ<,过Q作QC⊥PA,垂足为C,则∠PQC=|-θ|,
∴λ====.12分
由<θ<得,<sin θ≤1,故λ∈[,].14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com