
题目列表(包括答案和解析)
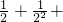 …+
…+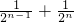 结果时,发现可利用图形的知识来解决问题.他是这样规定的:在图1中,若线段AB的长为1,C1为AB的中点,C2为C1B的中点,C3 为C2B的中点,…,Cn为Cn-1B的中点.
结果时,发现可利用图形的知识来解决问题.他是这样规定的:在图1中,若线段AB的长为1,C1为AB的中点,C2为C1B的中点,C3 为C2B的中点,…,Cn为Cn-1B的中点.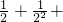 …+
…+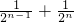 =________;
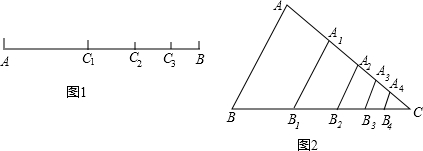
=________;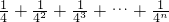 时,也可以利用构造一个图形,通过面积来计算.他构造图形是:如图2,正△ABC面积为1,分别取AC、BC两边的中点A1、B1,再分别取A1C、B1C的中点A2、B2,依次取下去…,能直观地计算出结果.请你根据这个图形说明小明的结果:
时,也可以利用构造一个图形,通过面积来计算.他构造图形是:如图2,正△ABC面积为1,分别取AC、BC两边的中点A1、B1,再分别取A1C、B1C的中点A2、B2,依次取下去…,能直观地计算出结果.请你根据这个图形说明小明的结果: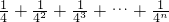 =________.
=________.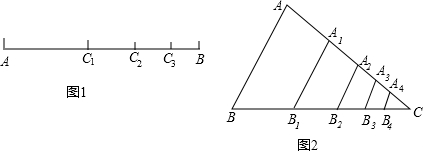
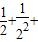 …+
…+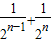 结果时,发现可利用图形的知识来解决问题.他是这样规定的:在图1中,若线段AB的长为1,C1为AB的中点,C2为C1B的中点,C3 为C2B的中点,…,Cn为Cn-1B的中点.
结果时,发现可利用图形的知识来解决问题.他是这样规定的:在图1中,若线段AB的长为1,C1为AB的中点,C2为C1B的中点,C3 为C2B的中点,…,Cn为Cn-1B的中点.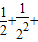 …+
…+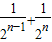 =______;
=______;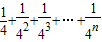 时,也可以利用构造一个图形,通过面积来计算.他构造图形是:如图2,正△ABC面积为1,分别取AC、BC两边的中点A1、B1,再分别取A1C、B1C的中点A2、B2,依次取下去…,能直观地计算出结果.请你根据这个图形说明小明的结果:
时,也可以利用构造一个图形,通过面积来计算.他构造图形是:如图2,正△ABC面积为1,分别取AC、BC两边的中点A1、B1,再分别取A1C、B1C的中点A2、B2,依次取下去…,能直观地计算出结果.请你根据这个图形说明小明的结果: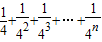 =______.
=______.
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| 4 |
| 1 |
| 42 |
| 1 |
| 43 |
| 1 |
| 4n |
| 1 |
| 4 |
| 1 |
| 42 |
| 1 |
| 43 |
| 1 |
| 4n |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com