
题目列表(包括答案和解析)
| ||
| n个 |
| 1 |
| 3 |
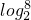 log=3(即
log=3(即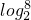 =3).
=3). 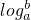 (即
(即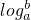 =n),如34=81,则指数4叫做以3为底81的对数,记为
=n),如34=81,则指数4叫做以3为底81的对数,记为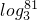 (即
(即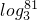 =4).
=4).阅读下列材料,并解决后面的问题.
材料:一般地,n个相同的因数相乘,记为an.如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底的对数,记为logab(即logab=n).若34=81,则4叫做以3为底81的对数,记为log381(即log381=4).问题:
(1)计算以下各对数的值:log24=________,log216=________,log264=________;
(2)观察(1)中三数4,16,64之间满足怎样的关系式?log24,log216,log264之间又满足怎样的关系式?
(3)由(2)的结果,你能归纳出一个一般性的结论吗?logaM+logaN=________(a>0且a≠1,M>0,N>0);
(4)根据幂的运算法则:an·am=an+m以及对数的含义证明上述结论。
阅读下列材料,并解决后面的问题.
材料:一般地,n个相同的因数相乘,记为an.如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底的对数,记为logab(即logab=n).若34=81,则4叫做以3为底81的对数,记为log381(即log381=4).问题:
(1)计算以下各对数的值:log24=________,log216=________,log264=________;
(2)观察(1)中三数4,16,64之间满足怎样的关系式?log24,log216,log264之间又满足怎样的关系式?
(3)由(2)的结果,你能归纳出一个一般性的结论吗?logaM+logaN=________(a>0且a≠1,M>0,N>0);
(4)根据幂的运算法则:an·am=an+m以及对数的含义证明上述结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com