
题目列表(包括答案和解析)
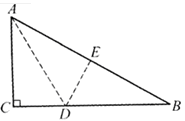
在如图所示的三角形纸片ABC中,∠C=90°,∠B=30°,按如下步骤可以把这个直角三角形纸片分成三个全等的小直角三角形(图中虚线表示折痕).①先将点B对折到点A,②将对折后的纸片再沿AD对折.
(1)由步骤①可以得到哪些等量关系?
(2)请证明△ACD≌△AED;
(3)按照这种方法能否将任意一个直角三角形分成三个全等的小三角形?
如图①所示,将一个正三角形纸片沿着它的一条边上的高剪开,得到如图②所示的两个全等的Rt△ABC、Rt△DEF.

(1)根据正三角形的性质可知:在图②中,∠ABC=∠DEF=30°,AB=DE=2AC=2DF.由此请你归纳一下在含30°角的直角三角形中,30°角所对的直角边与斜边之间的关系:
在含30°角的直角三角形中,30°角所对的直角边________;
(2)将这两个直角三角形纸片按如图③放置,使点B、D重合,点F在BC上.固定纸片DEF,将△ABC绕点F逆时针旋转角α(0°<α<90°),使四边形ACDE为以ED为底的梯形(如图④所示),求此时α的值;
(3)猜想图④中AE与CD之间的大小关系,并说明理由.
下图①是边长分别为4![]() 和3的两个等边三角形纸片ABC和
和3的两个等边三角形纸片ABC和![]() 叠放在一起(C与
叠放在一起(C与![]() 重合).
重合).
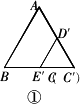
(1)操作:固定△ABC,将△![]() 绕点C顺时针旋转30°得到△CDE,连接AD、BE,CE的延长线交AB于点F(如图②).
绕点C顺时针旋转30°得到△CDE,连接AD、BE,CE的延长线交AB于点F(如图②).
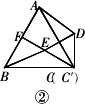
探究:在图②中,线段BE与AD之间有怎样的大小关系?试证明你的结论.
(2)操作:将图②中的△CDE,在线段CF上沿着CF方向以每秒1个单位的速度平移,CF为∠ACB的平分线,平移后的△CDE设为△PQR(如图③).
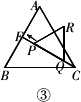
探究:设△PQR移动的时间为xs,△PQR与△AFC重叠部分的面积为y,求y与x之间的函数关系式,并写出函数自变量x的取值范围.
(3)操作:将图①中△![]() 固定,将△ABC移动,使顶点C落在
固定,将△ABC移动,使顶点C落在![]() 的中点,边BC交
的中点,边BC交![]() 于点M,边AC交
于点M,边AC交![]() 于点N,设∠AC
于点N,设∠AC![]() =α(30°<α<90°)(如图④).
=α(30°<α<90°)(如图④).
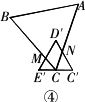
探究:在图④中,线段![]() N·
N·![]() M的值是否随α的变化而变化?如果没有变化,请求出
M的值是否随α的变化而变化?如果没有变化,请求出![]() N·
N·![]() M的值;如果有变化,请说明理由.
M的值;如果有变化,请说明理由.
刘卫同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.图①中,∠B=90°,∠A=30°,BC=6 cm;图②中,∠D=90°,∠E=45°,DE=4 cm.图③是刘卫同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).

(1)在△DEF沿AC方向移动的过程中,刘卫同学发现:F、C两点间的距离逐渐________.
(填“不变”、“变大”或“变小”)
(2)刘卫同学经过进一步地研究,编制了如下问题:
问题①:当△DEF移动至什么位置,即AD的长为多少时,F、C的连线与AB平行?
问题②:当△DEF移动至什么位置,即AD的长为多少时,以线段AD、FC、BC的长度为三边长的三角形是直角三角形?
问题③:在△DEF的移动过程中,是否存在某个位置,使得∠FCD=15°?如果存在,
求出AD的长度;如果不存在,请说明理由.
请你分别完成上述三个问题的解答过程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com