
题目列表(包括答案和解析)
某工厂家具车间造A,B两类型桌子,每张桌子需木工和漆工两道工序完成,已知木工做一张A,B型的桌子分别需要1小时和2小时,漆工油漆一张A,B型的桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A,B型的桌子分别获利润2千元和3千元,试问工厂每天应生产A,B型的桌子各多少张时,才能获利润最大?
如图,已知⊙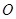 中,直径
中,直径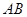 垂直于弦
垂直于弦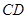 ,垂足为
,垂足为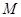 ,
,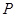 是
是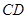 延长线上一点,
延长线上一点,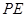 切⊙
切⊙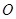 于点
于点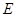 ,连接
,连接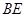 交
交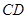 于点
于点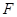 ,证明:
,证明: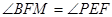
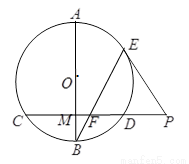
【解析】本试题主要考查了直线与圆的位置关系的运用。要证明角相等,一般运用相似三角形来得到,或者借助于弦切角定理等等。根据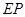 为⊙
为⊙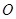 的切线,∴
的切线,∴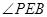 为弦切角
为弦切角
连接 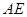 ∴
∴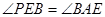 …注意到
…注意到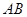 是直径且垂直弦
是直径且垂直弦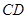 ,所以
,所以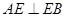 且
且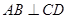 …利用
…利用 ,可以证明。
,可以证明。
解:∵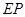 为⊙
为⊙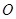 的切线,∴
的切线,∴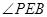 为弦切角
为弦切角
连接 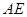 ∴
∴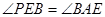 ……………………4分
……………………4分
又∵ 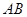 是直径且垂直弦
是直径且垂直弦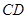 ∴
∴ 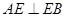 且
且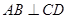 ……………………8分
……………………8分
∴  ∴
∴ 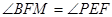
在 中,已知
中,已知
 ,面积
,面积 ,
,
(1)求 的三边的长;
的三边的长;
(2)设 是
是 (含边界)内的一点,
(含边界)内的一点, 到三边
到三边 的距离分别是
的距离分别是
①写出 所满足的等量关系;
所满足的等量关系;
②利用线性规划相关知识求出 的取值范围.
的取值范围.
【解析】第一问中利用设 中角
中角 所对边分别为
所对边分别为
由 得
得
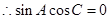

又由 得
得 即
即

又由 得
得 即
即

又
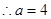 又
又 得
得
即 的三边长
的三边长

第二问中,① 得
得

故
②
令 依题意有
依题意有
作图,然后结合区域得到最值。

在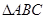 中,已知
中,已知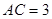 ,
, ;
;
(1)求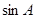 的值;(2)若
的值;(2)若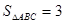 ,求
,求 的值;
的值;
【解析】第一问中,利用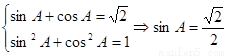
第二问中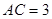 即
即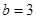 又
又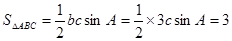

再有余弦定理解得。
解:(1)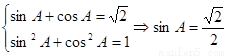 ……4分
……4分
(2)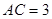 即
即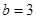
又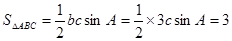
 ……8分
……8分
又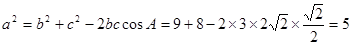
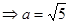 即
即 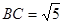
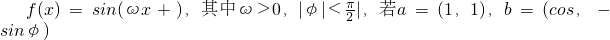 ,且
,且 ⊥
⊥ ,又知函数
,又知函数 个单位得到g(x)的图象,求g(x)的单调递增区间.
个单位得到g(x)的图象,求g(x)的单调递增区间.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com