
题目列表(包括答案和解析)
设椭圆 的离心率
的离心率 ,右焦点到直线
,右焦点到直线 的距离
的距离
 O为坐标原点。
O为坐标原点。
(I)求椭圆C的方程;
(II)过点O作两条互相垂直的射线,与椭圆C分别交于A,B两点,证明: 点O到直线AB的距离为定值,并求弦AB长度的最小值。
 的离心率
的离心率 ,右焦点到直线
,右焦点到直线 的距离
的距离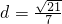 ,O为坐标原点.
,O为坐标原点.设椭圆![]() 的离心率
的离心率![]() ,右焦点到直线
,右焦点到直线![]() 的距离
的距离![]() O为坐标原点. (I)求椭圆C的方程; (II)过点O作两条互相垂直的射线,与椭圆C分别交于A,B两点,证明点O到直线AB的距离为定值,并求弦AB长度的最小值.
O为坐标原点. (I)求椭圆C的方程; (II)过点O作两条互相垂直的射线,与椭圆C分别交于A,B两点,证明点O到直线AB的距离为定值,并求弦AB长度的最小值.
设椭圆![]() 的离心率
的离心率![]() ,右焦点到直线
,右焦点到直线![]() 的距离
的距离![]() O为坐标原点. (I)求椭圆C的方程; (II)过点O作两条互相垂直的射线,与椭圆C分别交于A,B两点,证明点O到直线AB的距离为定值,并求弦AB长度的最小值.
O为坐标原点. (I)求椭圆C的方程; (II)过点O作两条互相垂直的射线,与椭圆C分别交于A,B两点,证明点O到直线AB的距离为定值,并求弦AB长度的最小值.
 的离心率
的离心率 ,右焦点到直线
,右焦点到直线 的距离
的距离 ,O为坐标原点.
,O为坐标原点.
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
B
A
C
A
B
D
B
D
C
A
C
二、填空题
13.30° 14..files/image163.gif) 15.-0.61 16.
15.-0.61 16..files/image165.gif)
三、解答题
17.解:(I).files/image110.gif)
即.files/image168.gif) 中出现3个1,2个0
2分
中出现3个1,2个0
2分
所以.files/image170.gif) 6分
6分
(II)(法一)设Y=X-1,
由题知.files/image172.gif) 9分
9分
所以.files/image174.gif) 12分
12分
(法二)X的分布列如下:
X
1
2
3
4
P(X)
.files/image176.gif)
.files/image178.gif)
.files/image180.gif)
.files/image182.gif)
X
5
6
P(X)
.files/image184.gif)
.files/image186.gif)
……10服
所以.files/image188.gif) …………12分
…………12分
18.解:(I)由三视图可得,三棱锥A―BCD中
.files/image190.gif) 都等于90°,
都等于90°,
每个面都是直角三角形;
可得.files/image192.gif) 面ADB,所以
面ADB,所以.files/image194.gif) ……2分
……2分
又.files/image196.gif) ,所以
,所以.files/image198.gif) 面ABC,
面ABC,
所以DE.files/image200.gif) AC, 4分
AC, 4分
又DF.files/image200.gif) AC,所以AC
AC,所以AC.files/image200.gif) 面DEF。
6分
面DEF。
6分
(II)方法一:由(I)知.files/image202.gif) 为二面角B―AC―D的平面角, 9分
为二面角B―AC―D的平面角, 9分
|