
求 的值.
的值.
求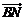 的长;
的长;
 ,棱
,棱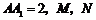 分别是
分别是 的中点.
的中点.
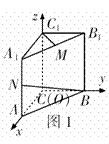
例13、如图1,直三棱柱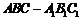 中,
中,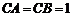 ,
,

【命题规律】空间向量的问题一般出现在立体几何的解答题中,难度为中等偏难.
(2)设 ,
, ,求点
,求点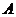 到平面
到平面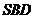 的距离;
的距离;
考点六:空间向量(理科)
【内容解读】用空间向量解决立体几何问题的“三步曲”
(1)用空间向量表示问题中涉及的点、直线、平面,建立立体图形与空间向量的联系,从而把立体几何问题转化为向量问题(几何问题向量化);
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹我有等问题(进行向量运算);
(3)把向量的运算结果“翻译”成相应的几何意义(回归几何问题).
(1)求证:平面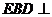 平面
平面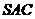 ;
;
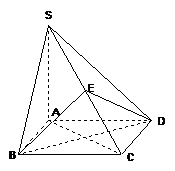 例12、(2008广东深圳模拟)如图,四棱锥
例12、(2008广东深圳模拟)如图,四棱锥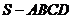 的底面是正方形,
的底面是正方形,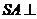 底面
底面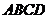 ,
,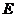 是
是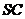 上一点.
上一点.
 (I) 求证:平面PDC
(I) 求证:平面PDC 平面PAD;
平面PAD;
(II) 求证:BE//平面PAD.
例11、(2008广东中山模拟)如图,四棱锥P―ABCD中, PA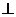 平面ABCD,底面ABCD是直角梯形,AB⊥AD,CD⊥AD,CD=2AB,E为PC中点.
平面ABCD,底面ABCD是直角梯形,AB⊥AD,CD⊥AD,CD=2AB,E为PC中点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com