2．等分线段找等势点法：将电势最高点和电势最低点连接后根据需要平分成若干段，必能找到第三点电势的等势点，它们的连线即等势面(或等势线)，与其垂直的线即为电场线．

突破训练3　如图9所示，匀强电场中有a、b、c三点，在以它们为顶点的三角形中，∠a＝30°，∠c＝90°.电场方向与三角形所在平面平行．已知a、b和c点的电势分别为(2－) V、(2＋) V和2 V．该三角形的外接圆上最低、最高电势分别为　　　　　 (　)

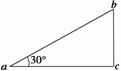
图9

A．(2－) V、(2＋) V

B．0、4 V

C. V、 V

D．0、2 V

答案　B

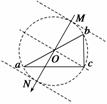解析　如图，圆心O是ab的中点，所以圆心O点的电势为2 V，

所以Oc是等势线，则电场线如图中MN所示，方向由M指向N.沿

电场线方向电势均匀降低，过圆心的电势为2 V，则圆周上电势最

低为0，最高为4 V，选B.

考点四　用功能关系分析带电粒子的能量转化

1．在匀强电场中，电势沿直线均匀变化，即直线上距离相等的线段两端的电势差值相等．

2．在非匀强电场中，不能用U＝Ed进行计算，但可以进行定性分析，一般沿电场线方向取相同的长度d，线段处于场强较大的区域所对应的电势差U较大．

例3　(2012·安徽·18)如图8所示，在平面直角坐标系中，有一个方向平行于坐标平面的匀强电场，其中坐标原点O处的电势为0 V，点A处的电势为6 V，点B处的电势为3 V，则电场强度的大小为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

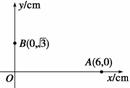
图8

A．200 V/m　 　　　　　　　　　　　　　 B．200 V/m

C．100 V/m　 　　　　　　　　　　　　　 D．100 V/m

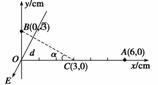
解析　在匀强电场中，沿某一方向电势降落，则在这一方向上电势均匀降落，故OA的中点C的电势φ_C＝3 V(如图所示)，因此BC为等势面．O点到BC的距离d＝OCsin α，而sin α＝＝，所以d＝OC＝1.5×10^－2 m．根据E＝得，匀强电场的电场强度E＝＝ V/m＝200 V/m，故选项A正确，选项B、C、D错误．

答案　A

1．在匀强电场中电势差与电场强度的关系式为U＝Ed，其中d为两点沿电场线方向的距离．由公式U＝Ed可以得到下面两个结论：

结论1：匀强电场中的任一线段AB的中点C的电势φ_C＝，如图7甲所示．

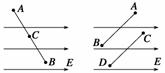
甲　　　乙

图7

结论2：匀强电场中若两线段AB∥CD，且AB＝CD，则U_AB＝U_CD(或φ_A－φ_B＝φ_C－φ_D)，如图乙所示．

2．带电粒子在电场中运动轨迹问题的分析方法

(1)从轨迹的弯曲方向判断受力方向(轨迹向合外力方向弯曲)，从而分析电场方向或电荷的正负；

(2)结合轨迹、速度方向与静电力的方向，确定静电力做功的正负，从而确定电势能、电势和电势差的变化等；

(3)根据动能定理或能量守恒定律判断动能的变化情况．

例2　如图5所示，一带电粒子在两个固定的等量正电荷的电场中运动，图中的实线为等势面，虚线ABC为粒子的运动轨迹，其中B点是两点电荷连线的中点，A、C位于同一等势面上．下列说法正确的是　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

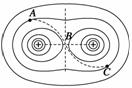
图5

A．该粒子可能带正电

B．该粒子经过B点时的速度最大

C．该粒子经过B点时的加速度一定为零

D．该粒子在B点的电势能小于在A点的电势能

解析　从该电荷的运动轨迹看，固定电荷对它有吸引力，由固定电荷带正电可知，该运动电荷一定带负电，故A错误；因为运动电荷从A到B的过程中，只受电场力且电场力先做正功后做负功，由动能定理知：动能先增加后减小，故B点的动能不是最大，则经过B点时的速度不是最大，故B错误；B点是两点电荷连线的中点，合场强为零，故运动电荷受力为零，则加速度为零，C正确；因为离正电荷越远，电势越低，即φ_A<φ_B，因粒子带负电，由E_p＝φq得，E_pA>E_pB，故D项正确．

答案　CD

　　　带电粒子运动轨迹类问题的解题技巧

(1)判断速度方向：带电粒子的轨迹的切线方向为该点处的速度方向．

(2)判断电场力(或场强)的方向：仅受电场力作用时，带电粒子所受电场力方向指向轨迹曲线的凹侧，再根据粒子的正负判断场强的方向．

(3)判断电场力做功的正负及电势能的增减：若电场力与速度方向成锐角，则电场力做正功，电势能减少；若电场力与速度方向成钝角，则电场力做负功，电势能增加．

突破训练2　如图6所示，A、B两点是粒子在匀强电场中运动时经过的两个点，平行直线表示电场线，但方向未知，整个过程中只有电场力做功．已知粒子在A点的动能比B点大，则下列说法中正确的是　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

图6

A．无论粒子是从A到B，还是从B到A，电场力均做负功

B．电场线方向从右向左

C．粒子的运动轨迹若为1，则粒子一定带负电

D．无论粒子是带正电还是负电，均不可能沿轨迹2运动

答案　D

解析　由于粒子在A点的动能比B点大，结合电场线与轨迹形状(质点做曲线运动时合力必指向凹侧)进行分析，若粒子沿轨迹1运动时，则在任意位置时粒子所受到的电场力一定水平向左，若粒子从A到B，则电场力做负功，从B到A，则电场力做正功，由此可知，A错误；此时若粒子带正电，电场方向一定向左，且由A向B运动，若粒子带负电，电场方向一定向右，且由B向A运动，均满足粒子在A点的动能比B点大．若粒子沿轨迹2运动时，则在任意位置时粒子所受到的电场力一定水平向右，同理可判断此情况下粒子在A点的动能一定比B点的小，不符合题意，即符合题意的粒子一定沿轨迹1运动，由此可知B、C错误，D选项正确．

考点三　匀强电场中电势差与电场强度的关系

1．几种常见的典型电场的等势面比较

电场	等势面(实线)图样	重要描述
匀强电场		垂直于电场线的一簇平面
点电荷的电场		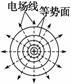以点电荷为球心的一簇球面
等量异种点电荷的电场		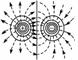连线的中垂线上的电势为零
等量同种正点电荷的电场		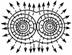连线上，中点电势最低，而在中垂线上，中点电势最高

2．电势能大小的比较方法

做功判断法

电场力做正功，电荷(无论是正电荷还是负电荷)从电势能较大的地方移向电势能较小的地方，反之，如果电荷克服电场力做功，那么电荷将从电势能较小的地方移向电势能较大的地方．

特别提醒　其他各种方法都是在此基础上推理出来的，最终还要回归到电场力做功与电势能的变化关系上．

例1　如图3所示，a、b、c、d分别是一个菱形的四个顶点，∠abc＝120°. 现将三个等量的正点电荷＋Q固定在a、b、c三个顶点上，将一个电荷量为＋q的点电荷依次放在菱形中心点O点和另一个顶点d点，两点相比　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

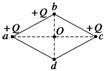
图3

A．＋q在d点所受的电场力较大

B．＋q在d点所具有的电势能较大

C．d点的电场强度大于O点的电场强度

D．d点的电势低于O点的电势

解析　a、c两个顶点的点电荷在菱形中心点O点产生的电场抵消，设b、O两点之间距离为x，则固定于b顶点的点电荷在菱形中心点O点产生的电场强度为kQ/x²；a、b、c三个顶点的点电荷在顶点d点产生的电场强度为kQ/(2x)²＋[2kQ/(2x)²]×cos 60°＝kQ/2x²，方向由O指向d，显然，d点电场强度比O点小，而F＝qE，则＋q在d点所受的电场力较小，选项A、C错误；根据沿着电场线方向电势逐渐降低的规律可知，O点电势高于d点，＋q在d点所具有的电势能较小，选项B错误，选项D正确．

答案　D

突破训练1　如图4所示，xOy平面内有一匀强电场，场强为E，方向未知，电场线跟x轴的负方向夹角为θ，电子在坐标平面xOy内，从原点O以大小为v₀、方向沿x轴正方向的初速度射入电场，最后打在y轴上的M点．电子的质量为m，电荷量为e，重力不计．则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

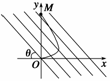
图4

A．O点电势高于M点电势

B．运动过程中，电子在M点电势能最大

C．运动过程中，电子的电势能先减少后增加

D．电场力对电子先做负功，后做正功

答案　D

解析　由电子的运动轨迹知，电子受到的电场力方向斜向左上，故电场方向斜向右下，M点电势高于O点电势，A错误；电子在M点电势能最小，B错误；运动过程中，电子先克服电场力做功，电势能增加，后电场力对电子做正功，电势能减少，故C错误，D正确．

考点二　电场线、等势面及带电粒子的运动轨迹问题

1．比较电势高低的方法

(1)沿电场线方向，电势越来越低．

(2)判断出U_AB的正负，再由U_AB＝φ_A－φ_B，比较φ_A、φ_B的大小，若U_AB>0，则φ_A>φ_B，若U_AB<0，则φ_A<φ_B.

4．电势差与电场强度的关系：匀强电场中两点间的电势差等于电场强度与这两点沿电场线方向的距离的乘积．即U＝Ed，也可以写作E＝.

考点一　电势高低及电势能大小的判断方法

3．电势差U_AB由电场中A、B两点的位置决定，与移动的电荷q、电场力做的功W_AB无关，与零电势点的选取也无关．