
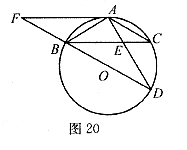
26.(本题10分)如图20所示,BD为⊙O的直径,AB=AC,AD交BC于E,AE=2,ED=4.
(1)求证: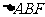 ∽
∽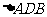 ,并求AB的长.
,并求AB的长.
(2)延长DB到F,使BF=BO,连接FA,那么直线FA与⊙O相切吗?为什么?
25.(本题12分)某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
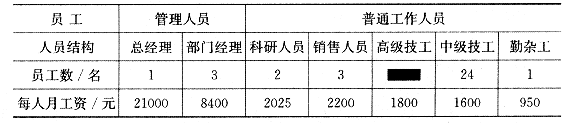
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名.
(2)所有员工月工资的平均数j为2500元,中位数为 元,众数为 元.
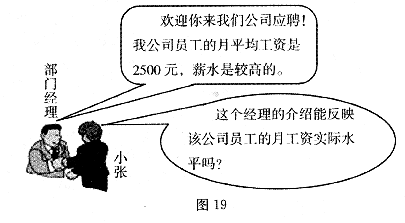
(3)小张到这家公司应聘普通工作人员.请你回答图19中小张的问题,并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些.
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资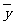 (结果保留整数),并判断
(结果保留整数),并判断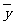 能否反映该公司员工的月工资实际水平.
能否反映该公司员工的月工资实际水平.
24.(每小题6分,满分12分)
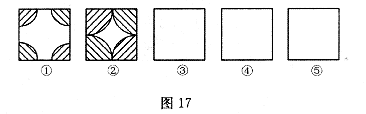
(1)为创建绿色校园,学校决定对一块正方形的空地进行种植花草,现向学生征集设计图案.图案要求只能用圆弧在正方形内加以设计,使正方形和所画的圆弧构成的图案,既是轴对称图形又是中心对称图形.种植花草部分用阴影表示.请你在图③、图④、图⑤中画出三种不同的设计图案.
提示:在两个图案中,只有半径变化而圆心不变的图案属于同一种,例如:图①、图②只能算一种。
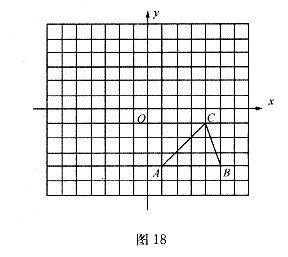
(2)如图18所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-l).
①把△ABC向上平移5个单位后得到对应的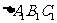 ,画出
,画出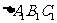 ,并写出点
,并写出点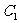 的坐标;
的坐标;
②以原点O为对称中心,再画出与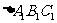 关于原点O对称的
关于原点O对称的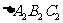 ,并写
,并写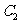 的坐标。
的坐标。
23.(本题10分)元旦联欢会前某班布置教室,同学们利用彩纸条粘成一环套一环的彩纸链,小颖测量了部分彩纸链的长度,她得到的数据如下表:

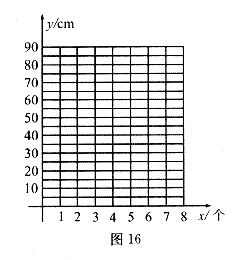
(1)把上表中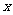 ,
,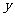 的各组对应值作为点的坐标,在如图16所示的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在如图16所示的平面直角坐标系中描出相应的点,猜想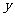 与
与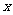 的函数关系,并求出函数关系式.
的函数关系,并求出函数关系式.
(2)教室天花板对角线长10m,现需沿天花板对角线各拉一根彩纸链,则每根彩纸链至少用多少个纸环?
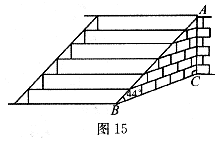
22.(本题8分)如图15所示,武当山风景管理区为提高游客到某景点的安全性,决定将到达该景点的步行台阶进行改善,把倾角由44º减至32º,已知原台阶AB的长为5m(BC所在地面为水平面).
(1)改善后的台阶会加长多少?(精确到0.01m)
(2)改善后的台阶多占多长的一段地面?(精确到0.01m)
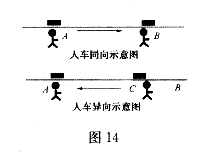
21.(本题8分)某人在电车路轨旁与路轨平行的路上骑车行走,他留意到每隔6分钟有一部电车从他后面驶向前面,每隔2分钟有一部电车从对面驶向后面.假设电车和此人行驶的速度都不变(分别为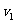 ,
,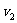 ),请你根据下面的示意图,求电车每隔几分钟(用t
),请你根据下面的示意图,求电车每隔几分钟(用t
20.(本题6分)解分式方程: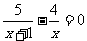
19.(本题6分)请你从下列各式中,任选两式作差,并将得到的式子进行因式分解.
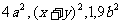
18.现有若干张边长不相等但都大于4cm的正方形纸片,从中任选一张,如图13所示,从距离正方形的四个顶点2cm处,沿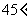 角画线,将正方形纸片分成5部分,则中间阴影部分的面积是
角画线,将正方形纸片分成5部分,则中间阴影部分的面积是 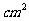 ;若在上述正方形纸片中再任选一张重复上述过程,并计算阴影部分的面积,你能发现什么规律?
;若在上述正方形纸片中再任选一张重复上述过程,并计算阴影部分的面积,你能发现什么规律?
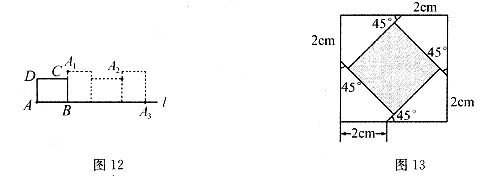
17.如图12所示,矩形ABCD中,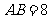 ,
,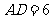 ,将矩形ABCD在直线
,将矩形ABCD在直线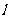 上按顺时针方向不滑动地每秒转动
上按顺时针方向不滑动地每秒转动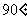 ,转动3s后停止,则顶点A经过的路线长为 .
,转动3s后停止,则顶点A经过的路线长为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com