
6.某公园计划砌一个形状如图4a所示的喷水池,后来有人建议改为图4b的形状,且外圆的直径不变,喷水池边沿的宽度、高度不变,你认为砌喷水池的边沿
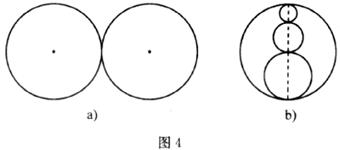
A.图5a需要的材料多 B.图5b需要的材料多
C.图5a、图5b需要的材料一样多 D.无法确定
5.图3是5个城市的国际标准时间(单位:时),那么北京时间2007年6月17 日上午9时应是

A.伦敦时间2007年6月17日凌晨1时
B.纽约时间2007年6月17日晚上22时
C.多伦多时间2007年6月16日晚上20时
D.汉城时间2007年6月17日上午8时
4.如图2所不,把直线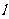 向上平移2个单位得到直线
向上平移2个单位得到直线 ,则
,则 的表达式为
的表达式为
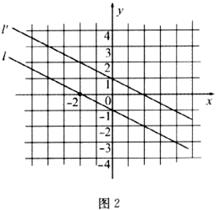
A. B.
B.
C.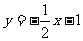 D.
D.
3.下列成语所描述的事件是必然事件的是
A.水中捞月 B.拔苗助长
C.守株待兔 D.瓮中捉鳖
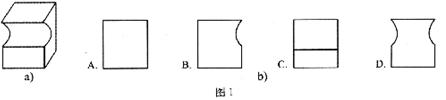
2.图1a所示几何体的左视图是图1b中的
下列各题都有代号为A、B、C、D的四个结论供选择,其中只有一个结论是正确的。
1.下列各式中,与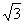 是同类根式的是
是同类根式的是
A. B.24 C.
B.24 C. D.
D.
28.(本小题满分12分)
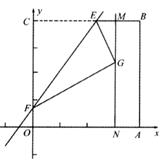
如图所示,四边形OABC是一张放在平面直角坐标系中的正方形纸片.点O与坐标原点重合,点A在 轴上,点C在y轴上,OC=4,点E为BC的中点,点N的坐标为(3,0),过点N且平行于y轴的直线MN与EB交于点M.现将纸片折叠,使顶点C落在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点。
轴上,点C在y轴上,OC=4,点E为BC的中点,点N的坐标为(3,0),过点N且平行于y轴的直线MN与EB交于点M.现将纸片折叠,使顶点C落在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点。
(1)求点G的坐标.
(2)求折痕EF所在直线的解析式.
(3)设点P为直线EF上的点,是否存在这样的点P,使得以P,F,G为顶点的三角形为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
27.(本小题满分11分)
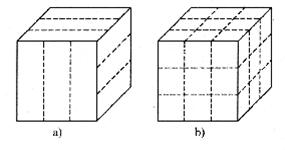
有一块表面是咖啡色,内部是白色,形状是正方体的烤面包,小明用刀在它的上表面、 前表面和右侧表面沿虚线各切两刀,如图a所示,将它切成若干块小正方体形面包,如图b所示.
(1)小明从若干块小面包中任取一块,求该块面包有且只有两个面是咖啡色的概率.
(2)小明和弟弟边吃边玩,游戏规则是:从中任取一块小面包,若它有奇数个面为咖啡色时,小明赢;否则弟弟赢.你认为这样的游戏规则公平吗?为什么?如果不公平,请你修改游戏规则,使之公平.
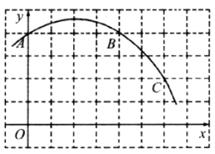
26.(本小题满分11分)如图所示,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C
(1)用直尺画出该圆弧所在圆的圆心M的位置.
(2)若A点的坐标为(0,4),D点的坐标为(7,0),试验证点D是否在经过点A、B、C的抛 物线上.
(3)在(2)的条件下,求证直线CD是⊙M的切线。
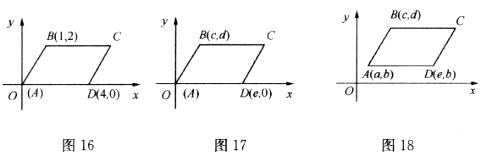
25.(本题12分)(1)在图16,17,18中,给出平行四边形ABCD的顶点A,B,D的坐标(如图所示),写出图16,17,18中的顶点C的坐标,它们分别是(5,2), ,
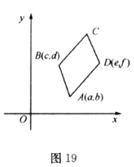
(2)在图19中,给出平行四边形ABCD的顶点A,B,D的坐标(如图所示),求出顶点C的坐标(C点坐标用含a,b,c,d,e,f的代数式表示);
归纳与发现.
(3)通过对图16,17,18,19的观察和顶点C的坐标的探究,你会发现:无论平行四边形ABCD处于直角坐标系中哪个位置,当其顶点坐标为A(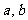 ),B(
),B(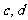 ),C(
),C(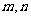 ),D(
),D(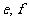 )(如图19)时,则四个顶点的横坐标
)(如图19)时,则四个顶点的横坐标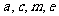 之间的等量关系为 ;纵坐标
之间的等量关系为 ;纵坐标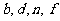 之间的等量关系为 (不必证明).
之间的等量关系为 (不必证明).
运用与推广
(4)在同一直角坐标系中有抛物线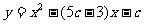 和三个点G(
和三个点G(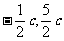 ),S(
),S(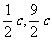 ),H(
),H(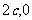 )(其中
)(其中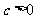 ).问当c为何值时,该抛物线上存在点P,使得以G,S,H,P为顶点的四边形是平行四边形?并求出所有符合条件的P点坐标.
).问当c为何值时,该抛物线上存在点P,使得以G,S,H,P为顶点的四边形是平行四边形?并求出所有符合条件的P点坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com