
例2 化简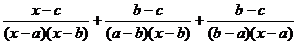
解析:本题直接通分非常困难,可考虑分步通分,即先将其中两个通分,待化简后再与第三个分式通分,这个题目后两个分式比较接近,我们可以考虑先把后两个分式通分.
解: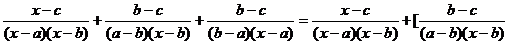 -
-

=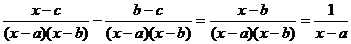
点拨:此解法适合于分式较多,分母逐次关连的分式化简
例1 化简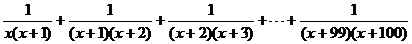
解析:本题直接化简非常困难,需要探究其规律求解,探究规律的方法可类比分数进行,下面我们先来解一道分数计算题.
计算: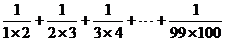
探究: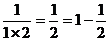
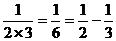
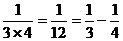 ……
……
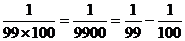 可猜想
可猜想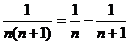 (n为正整数)
(n为正整数)
∴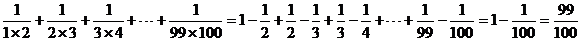
类比:这里分数分母中的两个因数相差1,而分式中分母的两个因式也是相差1,会不会有相同的规律呢?通过探究容易发现
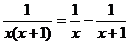
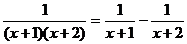 …
…
解答: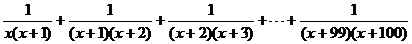
=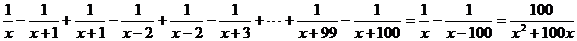
点拨:这种求和方法叫做“裂项求和法”
例4 计算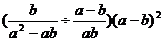
误解: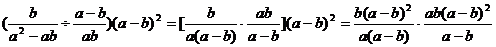
=b2(a-b)2
误区透析:误把乘法当加法,错用了分配律.
正解: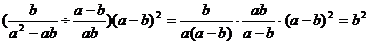
[巧思妙解]
分式化简求值有“巧”可取
例1 (2002·武汉)化简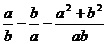 的结果是(
).
的结果是(
).
A.0
B.-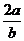 C.-
C.-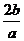 D.
D.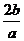
解析:本题用通分相减的办法可以解决,但比较麻烦,如果改用拆项的办法,将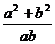 拆成
拆成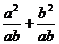 则计算更简洁.
则计算更简洁.
解: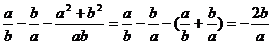 选C
选C
例2 (2005·福州)先化简,再求值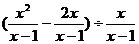 其中x=
其中x=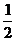
解析:本题若按运算顺序比较麻烦,若改用分配律则事半功倍.
解: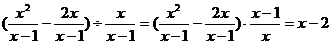
当x=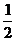 时,原式=-
时,原式=-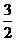
例3 (2005·潍坊)若x+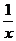 =3,求
=3,求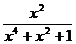 的值是( ).
的值是( ).
A.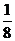 B.
B.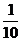 C.
C.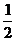 D.
D.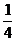
解析:本题若直接化简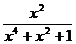 非常困难,如果把分子分母的位置颠倒,采用倒数法,则问题就可迎刃而解.
非常困难,如果把分子分母的位置颠倒,采用倒数法,则问题就可迎刃而解.
解: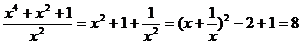
∴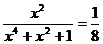
例4 已知a+b+c=0,求a(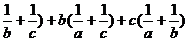 的值.
的值.
解析:本题初看无从下手,如将代数式“打散”重新组合,则易于解决
解:a(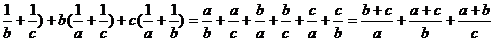
∵a+b+c=0 ∴a+b=-c a+c=-b b+c=-a
原式=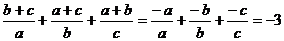
例5 先化简,再求值: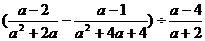 其中a满足:a2+2a-1=0
其中a满足:a2+2a-1=0
解析:本题没有直接给出a的值,而是一个方程,如果解出方程再代入求值十分困难,可以考虑整体代入法.
解: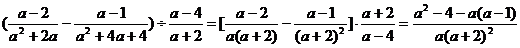
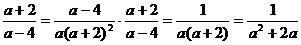
∵a2+2a-1=0 ∴a2+2a=1
∴原式=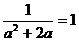
分式化简的方法探究举例
[思路点拨]
例3 计算: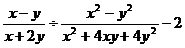
误解:
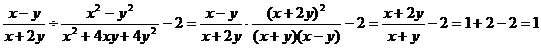
误区透析:误把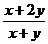 中的x、y当成公因式约分
中的x、y当成公因式约分
正解: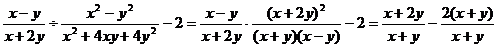
=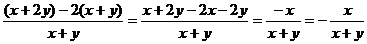
例2 计算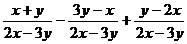
误解: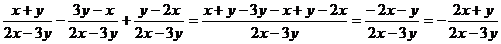
误区透析:忽视分子的整体性,忘记分数线的括号作用,因为漏添括号而出错.
正解:
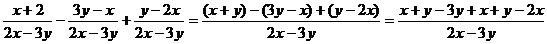
=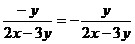
例1 计算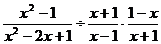
误解: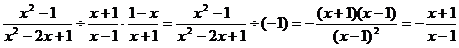
误区透析:认为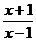 与
与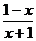 互为负倒数,乘积为-1,使计算简便,全然不讲运算顺序,结果弄巧成拙.
互为负倒数,乘积为-1,使计算简便,全然不讲运算顺序,结果弄巧成拙.
正解: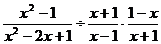
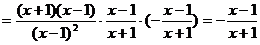
7、解: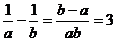 ,∴b-a=3ab,即a-b=-3ab;
,∴b-a=3ab,即a-b=-3ab;
∴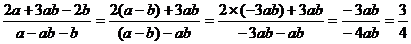
6、解: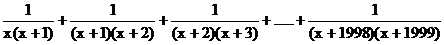
=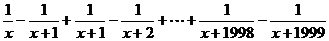
=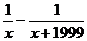
=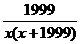
当x=1时,
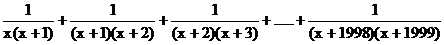
=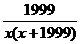 =
=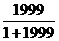 =
=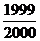
5、①(3);②不成立,分式的加减运算中不能“去分母”;
③正确的解答过程为:
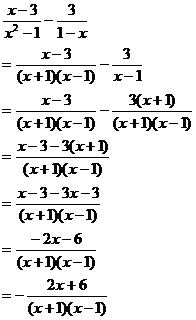
4、2;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com