
◆考点一、考查反比例函数概念
例1、小明家离学校 ,小明步行上学需 ,那么小明步行速度 可以表示为 ;水平地面上重 的物体,与地面的接触面积为 ,那么该物体对地面压强 可以表示为 ; ,函数关系式 还可以表示许多不同情境中变量之间的关系,请你再列举1例: .
析解:根据反比例函数的定义,由 可知y与x成反比例关系,因此可举例:"小红要完成1500个打字任务,那么小红每分钟打字个数y与打字时间x可表示为 "或"体积为1 500 的圆柱底面积为 ,那么圆柱的高 可以表示为 "(其它列举正确均可).
◆考点二、确定反比例函数的表达式
例2、 若反比例函数的图象过点 ,则其函数解析式为 .
析解:设所求反比例函数的解析式为 .
又由这个反比例函数的图象过点(-2,3),
所以 ,解得,k =-6. 故反比例函数的解析式为: .
◆考点三、反比例函数的图象和性质
例3 在反比例函数 图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是 ( )A
A.k>5 B.k>0 C.k<5 D. k<0
析解:由反比例函数y都随x的增大而减小可以判断图象分布在第一、三象限,因此比例系数k-5的符号是正数,解不等式k-5>0.即k>5,故应选A.
◆考点四、反比例函数与几何综合
例4、如图,反比例函数 的图象与直线 相交于
A、 B两点,AC∥ 轴,BC∥ 轴,则△ABC的面积等于 .
B、 个面积单位.
析解:A为的图像 上一点,S△AoD= k,由反比例函数关于原点的对称性
可知OA=OB,又AC∥ 轴,BC∥ 轴,
△ABC为等腰直角三角形,S△ABC=4 S△AOD =4× k =2k=10
◆考点五、反比例函数与一次函数综合
例5 已知 ,则函数 和 的图象大致是( )
析解:本题考查正比例函数和反比例函数的图象,因为 , 所以 分布在二、四象限;因为 ,所以 分布在一、三象限.故选D.
◆考点六、反比例函数与一次函数综合
在对物体做功一定的情况下,力F(牛)与此物体在力的方向上移动的距离s(米)成反比例函数关系,其图象如图4所示,P(5,1)在图象上,则当力达到10牛时,物体在力的方向上移动的距离是_______米.
析解:根据力F(牛)与此物体在力的方向上移动的距离s(米)成反比例函数关系,可设解析式为F= ,利用点P(5,1)在图象上,
求出解析式为F= ,当F=10时,s= =0.5
(1)一般地,形如 (k为常数,k≠0)的函数称为反比例函数,其中x是自变量,y是函数.反比例函数也可写成 的形式,其中自变量x≠0,常数k≠0.
(2)反比例函数 (k为常数,k≠0)的图象是双曲线;注意双曲线的两个分支不能与坐标轴相交.
(3)图象的性质:
①当k>0时,双曲线的两支分别位于第一、三象限,在每个象限内y随x的增大而减小;
②当k<0时,双曲线的两支分别位于第二、四象限,在每个象限内y随x的增大而增大.
(4)待定系数法确定函数解析式:一般知道了函数图象上任意一点的坐标,确定函数解析式,可采用待定系数法,即先设出函数解析式,然后将点的坐标代入确定系数.
例4 当k>0时,双曲线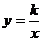 与直线y=-kx的交点的个数是 ( )
与直线y=-kx的交点的个数是 ( )
A.0个 B.1 个 C.2个 D.4个
分析:当k>0时, 双曲线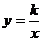 的两个分支分别位于第一、三象限,而直线y=-kx在第二、四象限,所以双曲线与直线没有公共点.即交点个数为0.
的两个分支分别位于第一、三象限,而直线y=-kx在第二、四象限,所以双曲线与直线没有公共点.即交点个数为0.
解:选A.
反比例函数复习引导
山东 康风星
例3 若点A(-3,y1),B(-2,y2),C(-1,y3)三点都在函数y=-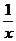 图象上,则y1,y2,y3的大小关系是( ).
图象上,则y1,y2,y3的大小关系是( ).
A.y1<y2<y3 B.y1=y2=y3 C.y1<y3<y2 D.y1>y2>y3.
分析:要比较y1,y2,y3的大小,解决问题的方法比较多,可以直接画出图象,通过观察点A、B、C 的位置比较大小,也可以通过代入法计算出函数,然后比较大小,也可以根据函数的性质直接比较大小.
解:因为点A、B、C都在函数y=-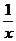 图象上,且都在函数图象上的第二象限的分支上,根据函数的性质:当k=-1<0时,y随x的增大而增大,可知y1<y2<y3,故选A.
图象上,且都在函数图象上的第二象限的分支上,根据函数的性质:当k=-1<0时,y随x的增大而增大,可知y1<y2<y3,故选A.
例2反比例函数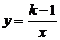 的图象在每个象限内,y随x的增大而减小,则k的值可为(
)
的图象在每个象限内,y随x的增大而减小,则k的值可为(
)
A.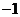 B.0
C.1
D.2
B.0
C.1
D.2
分析:要确定k的值,则需要依据反比例函数的性质.根据图象在每个象限内,y随x的增大而减小,可知k-1>0.
解:由已知,得k-1>0,所以k>1,观察四个选项,可知选D.
例1 反比例函数y=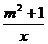 的图象的两个分支分别位于( )
的图象的两个分支分别位于( )
A.第一、三象限 B.第一、二象限 C.第二、四象限 D.第一、四象限
分析:要确定反比例函数图象的两个分支分别在第几象限,根据反比例函数的性质,只要确定m2+1的的符号即可.
解:因为m2+1>0,所以y=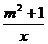 的图象的两个分支分别在第一、三象限.故选A.
的图象的两个分支分别在第一、三象限.故选A.
13,反比例函数的图象过点(2,-2),求函数y与自变量x之间的关系式,它的图象在第几象限内?y随x的减小如何变化?请画出函数图象,并判断点(-3,0),(-3,-3)是否在图象上?
14,若反比例函数y=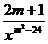 的图象经过第二、四象限,求函数的解析式.
的图象经过第二、四象限,求函数的解析式.
15,如图3所示,一个反比例函数的图象在第二象限内,点A是图象上的任意一点,AM⊥x轴于M,O是原点,若S△AOM=3,求该反比例函数的解析式,并写出自变量的取值范围.
16,点P,Q在y=-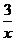 的图象上.
的图象上.
(1)若P(1,a),Q(2,b),比较a,b的大小;
(2)若P(-1,a),Q(-2,b),比较a,b的大小;
(3)你能从中发现y随x增大时的变化规律吗?
(4)若P(x1,y1),Q(x2,y2),x1<x2,你能比较y1与y2的大小吗?
17,(08达州市)平行于直线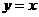 的直线
的直线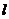 不经过第四象限,且与函数
不经过第四象限,且与函数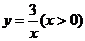 和图象交于点
和图象交于点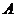 ,过点
,过点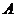 作
作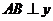 轴于点
轴于点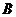 ,
,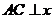 轴于点
轴于点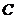 ,四边形
,四边形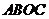 的周长为8.求直线
的周长为8.求直线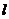 的解析式.
的解析式.
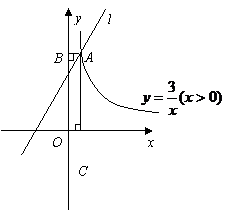
18,已知变量y与x成反比例,并且当x=2时,y=-3.
(1)求y与x的函数关系式;
(2)求当y=2时x的值;
(3)在直角坐标系内画出(1)小题中函数图象的草图.
7,已知反比例函数y=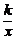 (k≠0)与一次函数y=x的图象有交点,则k的范围是______.
(k≠0)与一次函数y=x的图象有交点,则k的范围是______.
8,已知反比例函数y=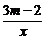 ,当m___时,其图象的两个分支在第二、四象限内;当m___时,其图象在每个象限内y随x的增大而减小.
,当m___时,其图象的两个分支在第二、四象限内;当m___时,其图象在每个象限内y随x的增大而减小.
9,若反比例函数y=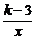 的图象位于一、三象限内,正比例函数y=(2k-9)x过二、四象限,则k的整数值是______.
的图象位于一、三象限内,正比例函数y=(2k-9)x过二、四象限,则k的整数值是______.
10,已知点P(1,a)在反比例函数y=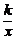 (k≠0)的图象上,其中a=m2+2m+3(m为实数),则这个函数的图象在第______象限.
(k≠0)的图象上,其中a=m2+2m+3(m为实数),则这个函数的图象在第______象限.
11,写出一个反比例函数,使它的图象在第二、 四象限,这个函数的解析式是_____.
12,已知反比例函数y=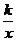 (k≠0),当x>0时,y随x的增大而增大,那么一次函数y=kx-k的图像过 象限.
(k≠0),当x>0时,y随x的增大而增大,那么一次函数y=kx-k的图像过 象限.
1,点A(-2,y1)与点B(-1,y2)都在反比例函数y=-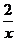 的图像上,则y1与y2的大小关系为( )
的图像上,则y1与y2的大小关系为( )
A.y1<y2 B.y1>y2 C.y1=y2 D.无法确定
2,若点(3,4)是反比例函数y=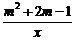 图象上一点,则此函数图象必经过点( )
图象上一点,则此函数图象必经过点( )
A.(2,6) B.(2,-6) C.(4,-3) D.(3,-4)
3,在函数y=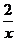 ,y=x+5,y=-5x的图像中,是中心对称图形,且对称中心是原点的图像的个数有( )
,y=x+5,y=-5x的图像中,是中心对称图形,且对称中心是原点的图像的个数有( )
A.0 B.1 C.2 D.3
4,已知函数y=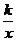 (k<0),又x1,x2对应的函数值分别是y1,y2,若x2>x1>0对,则有( )
(k<0),又x1,x2对应的函数值分别是y1,y2,若x2>x1>0对,则有( )
A.y1>y2>0 B.y2>y1>0 C.y1<y2<0 D.y2<y1<0
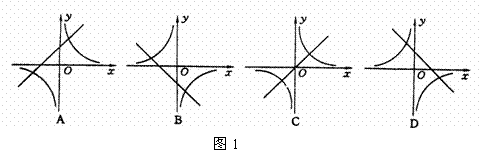
5,如图1,函数y=a(x-3)与y=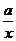 ,在同一坐标系中的大致图象是( )
,在同一坐标系中的大致图象是( )
6,如图2是三个反比例函数y=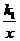 ,y=
,y=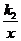 ,y=
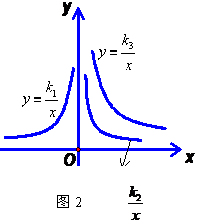
,y= 在x轴上方的图象,由此观察k1、 k2、k3得到的大小关系为( )
在x轴上方的图象,由此观察k1、 k2、k3得到的大小关系为( )
A.k1>k2>k3 B.k2>k3>k1 C.k3>k2>k1 D.k3>k1>k2

13,分别在坐标系中画出它们的函数图象.
(1)y=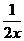 ;(2)y=-
;(2)y=-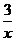 .
.
14,已知变量y与x成反比例,当x=3时,y=-6.
求:(1)y与x之间的函数关系式;(2)当 y=3时,x的值.
15,已知y=y1-y2,y1与x2成正比例,y2与x+3成反比例,当x=0时,y=2;当x=3时,y=0,求y与x的函数关系式,并指出自变量的取值范围.
16,已知函数y=ax和y=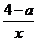 的图象有两个交点,其中一个交点的横坐标为1,则两个函数解析式分别是什么?
的图象有两个交点,其中一个交点的横坐标为1,则两个函数解析式分别是什么?
17,反比例函数y=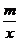 与一次函数y=kx+b的图象的一个交点为A(-2,-1),并且在x=3时,这两个函数的值相等,求这两个函数的解析式?
与一次函数y=kx+b的图象的一个交点为A(-2,-1),并且在x=3时,这两个函数的值相等,求这两个函数的解析式?
18,已知P是双曲线y=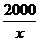 上的任意一点,过P分别作PA⊥x轴,PB⊥y轴,A,B分别是垂足.
上的任意一点,过P分别作PA⊥x轴,PB⊥y轴,A,B分别是垂足.
(1)求四边形PAOB的面积.
(2)P点向左移动时,四边形PAOB的面积如何变化?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com