
3、学生情况分析
我是一所山区中学的数学教师,我任教的班级学生基础一般,但学生学习积极性高,求知欲、表现欲强,具有一定的独立思考和探究的能力。但该班的学生在口头表达能力方面稍有欠缺,所以在本节课的教学过程中,我注重学生的说理能力、口头表达能力以及推理能力的培养。
2、教学重点难点
教学重点:正方形的概念和性质。
教学难点:理解正方形与平行四边形、菱形、矩形之间的内在联系及正方形的性质和应用。
1、教材的地位和作用
正方形在小学学生已经接触过。在现实生活中随处可见,应用非常广泛,它是学生非常熟悉的一种图形。《正方形》是在学生掌握了平行线、三角形、平行四边形、菱形、矩形等有关知识及轴对称图形和中心对称图形等平面几何知识,并且具备有初步的观察、操作、推理和证明等活动经验的基础上出现的。目的在于让学生通过探索正方形的性质,进一步学习、掌握说理、证明的数学方法。这一节课是前面所学知识的延伸和概括,充分体现了平行四边形、菱形、矩形、正方形这些概念之间的联系、区别和从属关系,同时又是高中阶段继续学习正方体、正六面体必备的知识。
2、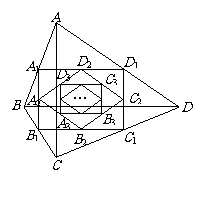 如图:四边形ABCD中,AC=6,BD=8且AC⊥BD顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1;再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2……如此进行下去得到四边形AnBnCnDn .
如图:四边形ABCD中,AC=6,BD=8且AC⊥BD顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1;再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2……如此进行下去得到四边形AnBnCnDn .
(1)证明:四边形A1B1C1D1是矩形;
(2)写出四边形A1B1C1D1和四边形A2B2C2D2的面积;
(3)写出四边形AnBnCnDn的面积;
(4)求四边形A5B5C5D5的周长.
学生板演
四 巩固练习,共同提高
(1)图①是一块直角三角形纸片。将该三角形纸片按如图方法折叠,是点A与点C重合,DE为折痕。试证明△CBE等腰三角形;
(2)再将图①中的△CBE沿对称轴EF折叠(如图②)。通过折叠,原三角形恰好折成两个重合的矩形,其中一个是内接矩形,另一个是拼合(指无缝无重叠)所成的矩形,我们称这样的两个矩形为“组合矩形”。你能将图③中的△ABC折叠成一个组合矩形吗?如果能折成,请在图③中画出折痕;
(3)请你在图④的方格纸中画出一个斜三角形,同时满足下列条件:①折成的组合矩形为正方形;②顶点都在格点(各小正方形的顶点)上;
(4)有一些特殊的四边形,如菱形,通过折叠也能折成组合矩形(其中的内接矩形的四个顶点分别在原四边形的四条边上)。请你进一步探究,一个非特殊的四边形(指除平行四边形、梯形外的四边形)满足何条件是,一定能折成组合矩形?

五 归纳总结,达成共识
师:本节课你们有什么收获和体会?
生14:我们学了当四边形为一般四边形时,中点四边形为平行四边形;
当原四边形对角线互相垂直时,中点四边形为矩形
当原四边形的对角线相等时,中点四边形是菱形
当原四边形的对角线相等且垂直时,中点四边形是正方形
师:还有补充的吗?
生15:中点四边形的面积是原四边形面积的一半。
生16:遇到与中点有关的问题时,可以构造中位线来解决。
六 作业布置:
1、已知四边形ABCD的中点四边形为正方形,则四边形ABCD 可能是下列图形中的那一种( )
A 等腰梯形 B 矩形 C 菱形 D 对角线互相垂直且相等的四边形
|
19.2
全等三角形的识别(4) |
|
|
1.探索两个直角三角形全等的识别方法 中的条件的个数:(除直角相等外)只 需两个(其中至少有一个条件是边相等) |
2.两个直角三角形全等的识别 方法,特别是(HL)的识别方法. |
2.实践探索
(1)实践活动
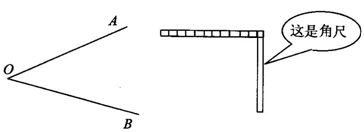
如图所示,木匠师傅常用角尺平分一个任意角.想想看,你能用图中的角尺平分∠AOB吗?你能用几种方法?
(2)巩固练习
①如图所示,AM是△ABC的BC边上的中线,CF⊥AM于F,BE⊥AM交AM的延长线于E.试说明BE=CF的理由.
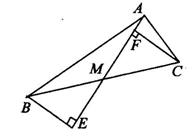
[答案] ∵BM=MC,∠BME=∠AMC,∴△BEM≌△CFM,∴BE=CF
②如图所示,已知AD是△ABC的角平分线,且BD=DC,DE、DF分别垂直于AB、AC,垂足分别为E、F,△BED≌△CFD吗?为什么?
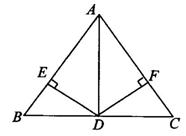
[答案] DE=DF,∴△BED≌△CFD(HL)
③过等腰直角三角形ABC的直角顶点C任画一条直线L,分别作AD⊥L,BE⊥L,垂足分别为D、E.
(a)试画出本题的图形.(提示:有两种不同的图形)
(b)在你所画的两种图形中分别说明△ACD≌△CBE的理由.
(c)若已知:AD=4cm,BE=3cm,求DE的长.
[答案] 略
1.链接生活
如图是公园里滑梯的平面图,已知两个滑梯的长度相同(即图中BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,你知道∠B与∠F有什么关系吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com