
3.巩固知识,强化能力
例1 求出图19.3.3所示的Rt△ABC中∠A的四个三角函数值.
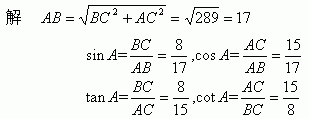
探 索
根据三角函数的定义,sin30゜是一个常数.用刻度尺量出你所用的含30゜的三角尺中,30゜所对的直角边与斜边的长,与同伴交流,看看这个常数是什么.
通过计算,我们可以得出
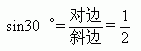
即斜边等于对边的2倍.因此我们还可以得到:
在直角三角形中,如果一个锐角等于30゜,那么它所对的直角边等于斜边的一半.
做一做
在Rt△ABC中,∠C=90゜,借助于你常用的两块三角尺,根据锐角三角函数定义求出∠A的四个三角函数值:
(1)∠A=30゜ (2)∠A=60゜ (3)∠A=45゜.
(可以通过画三角形来解决。)
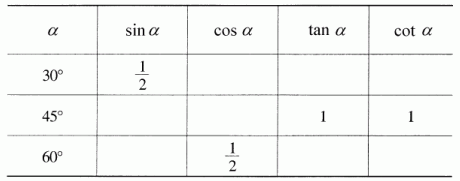
为了便于记忆,我们把30゜、45゜、60゜的三角函数值列表如下.(请填出空白处的值)
2.引入新知,形成概念
直角三角形ABC可以简记为Rt△ABC,我们已经知道,直角∠C所对的边AB称为斜边,用c表示,另两条直角边分别为∠A的对边与邻边,用a、b表示(如图19.3.1).
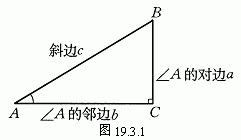
前面的结论告诉我们,在Rt△ABC中,只要一个锐角的大小不变(如∠A=34°),那么不管这个直角三角形大小如何,该锐角的对边与邻边的比值是一个固定的值.
思 考
一般情况下,在Rt△ABC中,当锐角A取其他固定值时,∠A的对边与邻边的比值还会是一个固定值吗?
观察图19.3.2中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,易知
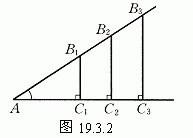
Rt△AB1C1∽Rt△_______∽Rt△_________.
所以
可见,在Rt△ABC中,对于锐角A的每一个确定的值,其对边与邻边的比值是惟一确定的.
我们同样可以发现,对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边的比值也是惟一确定的.
因此这几个比值都是锐角∠A的函数,记作sin A、cos A、tan A、cot A,即

分别叫做锐角∠A的正弦、余弦、正切、余切,统称为锐角∠A的三角函数.
显然,锐角三角函数值都是正实数,并且
0<sin A<1,0<cos A<1
根据三角函数的定义,我们还可得出
tan A•cot A=1
1. 复习巩固,做好铺垫
在19.1节中,我们曾经使用两种方法,求出操场旗杆的高度,其中都出现了两个相似的直角三角形,即
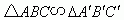
按1/500的比例,就一定有
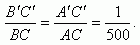
1/500就是它们的相似比.
当然也有 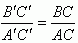
通过多媒体的演示,复习角的终边与始边,然后在终边上取一点P,切换至不同的位置,探究得
结论1:PM与OP的比始终等于定值,而与点P的在终边上的位置无关.
结论2:不论点P在终边上的位置如何,对于确定的锐角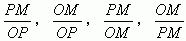 这四个比值都是定值,请猜想,什么条件变时,这四个比值会变?(a角度),由此知,这四个比值都是自变量a的函数.
这四个比值都是定值,请猜想,什么条件变时,这四个比值会变?(a角度),由此知,这四个比值都是自变量a的函数.
教学重点:锐角三角函数的概念及表示;
教学难点:锐角三角函数概念。
4.学会根据定义求锐角三角函数的值.
3.掌握直角三角形中的锐角三角函数;
2.掌握锐角三角函数的表示;
1.理解锐角三角函数概念;
19.2.3 正方形
|
教学目标 |
知识与技能 |
1.掌握正方形的概念、性质和判定,并会用它们进行有关的论证和计算. 2.理解正方形与平行四边形、矩形、菱形的联系和区别 |
|
过程与方法 |
经历探索正方形有关性质、判定重要条件的过程.在观察中寻求新知,在探索中发展推理能力,逐步掌握说理的基本方法. |
|
|
情感态度与价值观 |
通过正方形与平行四边形、矩形、菱形的联系的教学对学生进行辩证唯物主义教育,提高学生的逻辑思维能力. |
|
|
重点 |
正方形的定义及正方形与平行四边形、矩形、菱形的联系. |
|
|
难点 |
正方形与矩形、菱形的关系及正方形性质与判定的灵活运用. |
教学过程
|
备 注 |
教学设计 与 师生互动 |
|
|
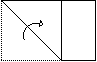 第一步:课堂引入 第一步:课堂引入1.做一做:用一张长方形的纸片(如图所示)折出一个正方形. 学生在动手做中对正方形产生感性认识,并感知正方形与矩形的关系.问题:什么样的四边形是正方形? 正方形定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形. 指出:正方形是在平行四边形这个大前提下定义的,其定义包括了两层意:  (1)有一组邻边相等的平行四边形 (菱形) (1)有一组邻边相等的平行四边形 (菱形)(2)有一个角是直角的平行四边形 (矩形) 2.[问题]正方形有什么性质? 由正方形的定义可以得知,正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形. 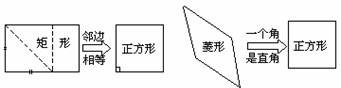 所以,正方形具有矩形的性质,同时又具有菱形的性质. 归纳、总结正方形的性质: 因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形,所以它具有这些图形性质的综合,引导学生从角、边、对角线上归纳总结. 正方形性质定理1:正方形的四个角都是直角,四条边都相等. 正方形性质定理2:正方形的两条对角线相等并且互相垂直平分,每一条对角线平分一组对角. |
第二步:应用举例: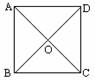 例1(教材P111的例4) 求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形. 例1(教材P111的例4) 求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.已知:四边形ABCD是正方形,对角线AC、BD相交于点O(如图).求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形. 证明:∵ 四边形ABCD是正方形, ∴ AC=BD, AC⊥BD, AO=CO=BO=DO(正方形的两条对角线相等,并且互相垂直平分). ∴ △ABO、△BCO、△CDO、△DAO都是等腰直角三角形, 并且 △ABO ≌△BCO≌△CDO≌△DAO. 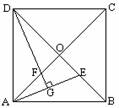 例2 (补充)已知:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.求证:OE=OF. 例2 (补充)已知:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.求证:OE=OF.分析:要证明OE=OF,只需证明△AEO≌△DFO,由于正方形的对角线垂直平分且相等,可以得到∠AOE=∠DOF=90°,AO=DO,再由同角或等角的余角相等可以得到∠EAO=∠FDO,根据ASA可以得到这两个三角形全等,故结论可得. 证明:∵ 四边形ABCD是正方形, ∴ ∠AOE=∠DOF=90°,AO=DO(正方形的对角线垂直平分且相等). 又 DG⊥AE, ∴ ∠EAO+∠AEO=∠EDG+∠AEO=90°. ∴ ∠EAO=∠FDO. ∴ △AEO ≌△DFO. ∴ OE=OF. 例3 (补充)已知:如图,四边形ABCD是正方形,分别过点A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB、DN分别交l2于Q、P点. 求证:四边形PQMN是正方形. 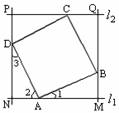 分析:由已知可以证出四边形PQMN是矩形,再证△ABM≌△DAN,证出AM=DN,用同样的方法证AN=DP.即可证出MN=NP.从而得出结论. 分析:由已知可以证出四边形PQMN是矩形,再证△ABM≌△DAN,证出AM=DN,用同样的方法证AN=DP.即可证出MN=NP.从而得出结论.证明:∵ PN⊥l1,QM⊥l1, ∴ PN∥QM,∠PNM=90°. ∵ PQ∥NM, ∴ 四边形PQMN是矩形. ∵ 四边形ABCD是正方形 ∴ ∠BAD=∠ADC=90°,AB=AD=DC(正方形的四条边都相等,四个角都是直角). ∴ ∠1+∠2=90°. 又 ∠3+∠2=90°, ∴ ∠1=∠3. ∴ △ABM≌△DAN. ∴ AM=DN. 同理 AN=DP. ∴ AM+AN=DN+DP 即 MN=PN. ∴ 四边形PQMN是正方形(有一组邻边相等的矩形是正方形). 例4:已知:分别延长等腰直角三角形OAB的两条直角边AO和BO ,使AO=OC,BO=OD,求证:四边形ABCD是正方形. 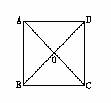
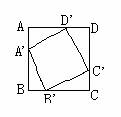 例5:已知:点A,、B,、C,、D,分别是正方形 ABCD四条边上的 点,并且AA,=BB,=CC,=DD.求证:四边形A,B,C,D,是正方形. |
|
|
第三步:、随堂练习 1.正方形的四条边____ __,四个角___ ____,两条对角线____ ____. 2.下列说法是否正确,并说明理由. 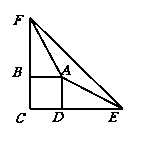 ①对角线相等的菱形是正方形;( ) ①对角线相等的菱形是正方形;( )②对角线互相垂直的矩形是正方形;( ) ③对角线垂直且相等的四边形是正方形;( ) ④四条边都相等的四边形是正方形;( ) ⑤四个角相等的四边形是正方形.( ) 1. 已知:如图,四边形ABCD为正方形,E、F分别 为CD、CB延长线上的点,且DE=BF.求证:∠AFE=∠AEF. 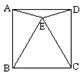 4.如图,E为正方形ABCD内一点,且△EBC是等边三角形,求∠EAD与∠ECD的度数. 4.如图,E为正方形ABCD内一点,且△EBC是等边三角形,求∠EAD与∠ECD的度数. |
|
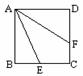 第四步:课后反思: 第四步:课后反思: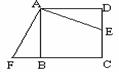 1.已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF. 1.已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.求证:EA⊥AF. 2.已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形. 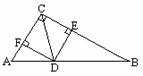 3.已知:如图,正方形ABCD中,E为BC上一点,AF平分∠DAE交CD于F,求证:AE=BE+DF. 3.已知:如图,正方形ABCD中,E为BC上一点,AF平分∠DAE交CD于F,求证:AE=BE+DF. |
|
|
第五步:反馈归纳 (1)正方形是怎样的平行四边形?,有一组邻边相等,且有一个角是直角的平行四边形; (2)正方形是怎样的矩形?有一组邻边相等的矩形; (3)正方形是怎样的菱形?有一个角是直角的菱形; (4)明确四者之间的关系!!!! (5)判定一个平行四边形是正方形,还应具备什么条件?方法1 (6)判定一个矩形是正方形还应具备什么条件?方法2; (7)判定一个菱形是正方形还应具备什么条件?方法3; (8)小结:判定正方形的方法有三种. 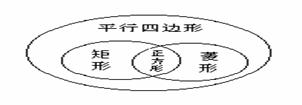 知识再现:   ⑴ 对边平行
边
⑴ 对边平行
边⑵ 四边相等  ⑶ 四个角都是直角
角
⑶ 四个角都是直角
角 正方形 ⑷ 对角线相等 正方形 ⑷ 对角线相等互相垂直 对角线 互相平分 平分一组对角 |
|
|
课后反思 : |
19.2.2 菱形(二)
|
教学目标 |
知识与技能 |
理解并掌握菱形的定义及两个判定方法;会用这些判定方法进行有关的论证和计算; |
|
过程与方法 |
经历探索菱形判定思想的过程,领会菱形的概念以及应用方法,发展学生主动探究的思想和说理的基本方法. |
|
|
情感态度与价值观 |
培养良好的思维意识以及合情推理的能力 ,感悟其应用价值及培养学生的观察能力、动手能力及逻辑思维能力. |
|
|
重点 |
菱形的两个判定方法. |
|
|
难点 |
判定方法的证明方法及运用. |
教学过程
|
备 注 |
教学设计 与 师生互动 |
|||||||||||||
|
|
第一步:课堂引入 1.复习 (1)菱形的定义:一组邻边相等的平行四边形; (2)菱形的性质1 菱形的四条边都相等; 性质2 菱形的对角线互相平分,并且每条对角线平分一组对角; (3)运用菱形的定义进行菱形的判定,应具备几个条件?(判定:2个条件) 2.[问题]要判定一个四边形是菱形,除根据定义判定外,还有其它的判定方法吗? 3.[探究](教材P109的探究)用一长一短两根木条,在它们的中点处固定一个小钉,做成一个可转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形? 通过演示,容易得到: 菱形判定方法1 对角线互相垂直的平行四边形是菱形. 注意此方法包括两个条件:(1)是一个平行四边形;(2)两条对角线互相垂直. 通过教材P109下面菱形的作图,可以得到从一般四边形直接判定菱形的方法: 菱形判定方法2 四边都相等的四边形是菱形. 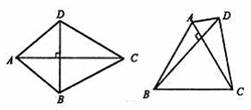 注意:应用判定方法1时,要注意其性质包括两个条件:(1)是一个平行四边形;(2)两条对角线互相垂直.如对角线互相垂直的四边形是菱形吗?为什么?同时可用图来证实,虽然对角线AC⊥BD,但它们都不是菱形. 注意:应用判定方法1时,要注意其性质包括两个条件:(1)是一个平行四边形;(2)两条对角线互相垂直.如对角线互相垂直的四边形是菱形吗?为什么?同时可用图来证实,虽然对角线AC⊥BD,但它们都不是菱形.菱形常用的判定方法归纳为(让学生讨论归纳后,并板书):  |
|||||||||||||
|
第二步:应用举例: 例1 (教材P109的例3)略 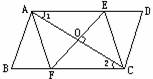 例2(补充)已知:如图 例2(补充)已知:如图 ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.求证:四边形AFCE是菱形. ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.求证:四边形AFCE是菱形.证明:∵ 四边形ABCD是平行四边形, ∴ AE∥FC. ∴ ∠1=∠2. 又 ∠AOE=∠COF,AO=CO, ∴ △AOE≌△COF. ∴ EO=FO. ∴ 四边形AFCE是平行四边形. 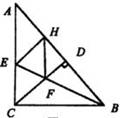 又 EF⊥AC, 又 EF⊥AC,∴  AFCE是菱形(对角线互相垂直的平行四边形是菱形). AFCE是菱形(对角线互相垂直的平行四边形是菱形).※例3(选讲) 已知:如图,△ABC中, ∠ACB=90°,BE平分∠ABC,CD⊥AB与D,EH⊥AB于H,CD交BE于F. 求证:四边形CEHF为菱形. 略证:易证CF∥EH,CE=EH,在Rt△BCE中,∠CBE+∠CEB=90°,在Rt△BDF中,∠DBF+∠DFB=90°,因为∠CBE=∠DBF,∠CFE=∠DFB,所以∠CEB=∠CFE,所以CE=CF. 所以,CF=CE=EH,CF∥EH,所以四边形CEHF为菱形. |
||||||||||||||
|
第三步:随堂练习 1.填空: (1)对角线互相平分的四边形是 ; (2)对角线互相垂直平分的四边形是________; (3)对角线相等且互相平分的四边形是________; (4)两组对边分别平行,且对角线 的四边形是菱形. 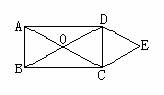 2.画一个菱形,使它的两条对角线长分别为6cm、8cm. 2.画一个菱形,使它的两条对角线长分别为6cm、8cm.3.如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E,求证:四边形OCED是菱形. |
||||||||||||||
第四步:课后练习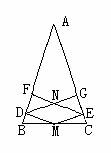 1.下列条件中,能判定四边形是菱形的是
( ). 1.下列条件中,能判定四边形是菱形的是
( ).(A)两条对角线相等 (B)两条对角线互相垂直 (C)两条对角线相等且互相垂直 (D)两条对角线互相垂直平分 2.已知:如图,M是等腰三角形ABC底边BC上的中点,DM⊥AB,EF⊥AB,ME⊥AC,DG⊥AC.求证:四边形MEND是菱形. 3.做一做: 设计一个由菱形组成的花边图案.花边的长为15 cm,宽为4 cm,由有一条对角线在同一条直线上的四个菱形组成,前一个菱形对角线的交点,是后一个菱形的一个顶点.画出花边图形. |
||||||||||||||
|
第五步:课堂小结: 菱形可根据哪些进行判定?填写下表、填图:
|
||||||||||||||
|
课后反思: |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com