3.已知cotA=3.1748,利用计算器求锐角A．(精确到1′)

2.用计算器求下式的值．(精确到0．0001)

sin81°32′17″+ cos38°43′47″.

1.不用计算器求下列锐角α的值：

(1)2sin(α-10°)=1；　　　

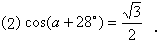
通过本节课的学习，我们既学会了利用计算器求出任意锐角的三角函数值，又能够反过来，由某个锐角的三角函数值求出这个锐角．

2.已知锐角α的三角函数值,使用计算机求锐角α.(精确到1′)

(1)sinα=0.2476；　　　 　(2)cosα=0.4174；

(3)tanα=0.1890；　　　　 (4)cotα=1.3773.

1.使用计算机求下列三角函数的值.(精确到0.0001)

sin24°,cos51°42′20″,tan70°21′,cot70°.

2.由锐角三角函数值求锐角

例4 已知tanx=0.7410,求锐角x.(精确到1′)

解　 在角度单位状态为“度”的情况下(屏幕显示出 D ),按下列顺序依次按键:

显示结果为36.538 445 77.

再按键:

显示结果为36 °32′18.4″.

所以　　 x≈36°32′ .

例5　 已知cotx=0.1950,求锐角x(精确到1′).

分析　 根据tanx·cotx=1,可求出tanx的值,然后根据例4的方法就可以求出锐角x的值.

练习

例1 根据下列条件，求出相应的锐角α：

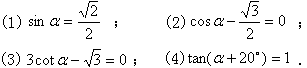
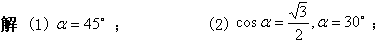
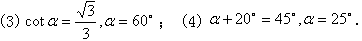
我们对特殊角的三角函数要能做到：已知一个锐角能正确说出它的三角函数值；已知一个锐角的三角函数值，能正确说出这个角的度数．

那如果这个角是任意的锐角呢？我们下面将介绍如何利用计算器求已知锐角的三角函数值和由三角函数值求对应的锐角．

1.求已知锐角的三角函数值

例2 求sin63°52′41″的值(精确到0.0001)．

解　 先用如下方法将角度单位状态设定为“度”:

显示结果为0.897 859 012

所以sin63°52′41″≈0.897 9.

例3 求cot70°45′.(精确到0.0001)

解　 在角度单位状态为“度”的情况下(屏幕显示出 D ),按下列顺序依次按键:

显示结果为0.349 215 633.

所以cot70°45′≈0.3492.

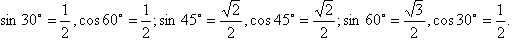
观察上面三种特殊角的正弦和余弦值，你有什么发现？

引导学生观察，由学生发现并得出sinα=cos(90°-α)、cosα=sin(90°-α)．引导学生考虑正切和余切也存在类似这样的关系吗？

归纳：sinα=cos(90°-α)、cosα=sin(90°-α)、

tanα= cot (90°-α) 、cotα=tan(90°-α),并用文字语言叙述出来．

我们知道锐角三角函数值都是正实数，如果∠α是锐角，则0＜sinα＜1，0＜cosα＜1，tanα·cotα=1．在上节课中，我们通过探索得到了30°、45°、60°的正弦、余弦、正切、余切值，你能把结论告诉大家吗？