
3.如图,在平面直角坐标系中,已知点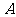 坐标为(2,4),直线x=2与x轴相交于点B,连结OA,抛物线
坐标为(2,4),直线x=2与x轴相交于点B,连结OA,抛物线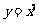 从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
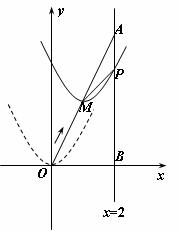
(1)求线段OA所在直线的函数解析式;
(2)设抛物线顶点M的横坐标为m,请用含m的代数式表示点P的坐标;
2.抛物线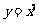 上有三点A、B、C,其横坐标分别是m、m+1、m+3,请你探究△ABC的面积S是否为定值,若是,请求出这个值;若不是,请你求出S与m的函数关系式.
上有三点A、B、C,其横坐标分别是m、m+1、m+3,请你探究△ABC的面积S是否为定值,若是,请求出这个值;若不是,请你求出S与m的函数关系式.
1.如下图是某宾馆大厅到二楼的楼梯设计图,已知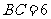 米,
米,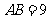 米,中间平台宽度
米,中间平台宽度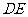 为2米,
为2米,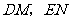 为平台的两根支柱,
为平台的两根支柱,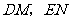 垂直于
垂直于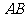 ,垂足分别为
,垂足分别为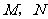 ,
,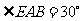 ,
,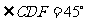 .
.
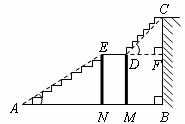
求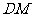 和
和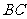 的水平距离
的水平距离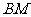 .(精确到0.1米,参考数据:
.(精确到0.1米,参考数据: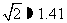 ,
,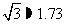 )
)
6.已知,点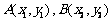 在抛物线
在抛物线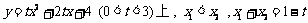
则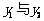 的大小关系是
的大小关系是
5.如图,在平面直角坐标系中,点A的坐标为(1,-2),点B的坐标为(3,-1),二次函数 的图象为
的图象为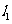 ,平移抛物线
,平移抛物线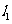 ,得到抛物线
,得到抛物线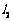 ,使
,使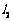 过点A,但不过点B,
过点A,但不过点B,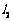 的顶点不是点A,请你写出抛物线
的顶点不是点A,请你写出抛物线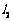 的一个解析式
(任写一个满足条件的即可). 平移抛物线
的一个解析式
(任写一个满足条件的即可). 平移抛物线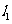 ,得到抛物线
,得到抛物线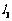 ,使
,使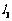 过点A,又过点B,请你写出抛物线
过点A,又过点B,请你写出抛物线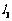 的一个解析式
的一个解析式
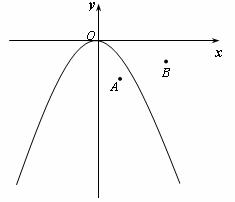
4.已知抛物线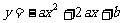 与
与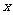 轴的一个交点为
轴的一个交点为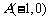 ,与y轴的正半轴交于点D.抛物线与
,与y轴的正半轴交于点D.抛物线与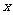 轴的另一个交点B的坐标是
轴的另一个交点B的坐标是
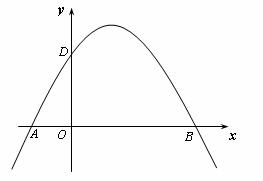
3.如下图,所示的两条抛物线的解析式分别是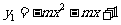 ,
,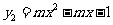 (其中m为常数,且
(其中m为常数,且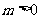 ).请写出三条与上述抛物线有关的不同类型的结论
;
).请写出三条与上述抛物线有关的不同类型的结论
;
; .
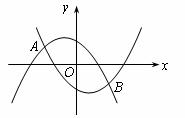
2.如下图,二次函数y=ax2+bx+c(a>0)与坐标轴交于点A、B、C且OA=1,OB=OC=3此二次函数的解析式为 .
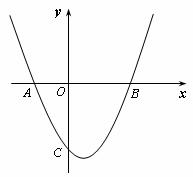
1.已知抛物线 经过点A(5,0)、B(6,-6)和原点,则抛物线的函数关系式是
.
经过点A(5,0)、B(6,-6)和原点,则抛物线的函数关系式是
.
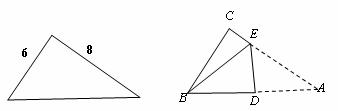
12.直角三角形纸片的两直角边长分别为6,8,现将△ABC如下图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是 ( )
A.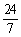 B.
B.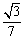 C.
C.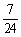 D.
D.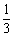
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com