
5. 夏令营活动中,田亮和李媛两位同学,同时从营地出发,步行15千米去完成老师交给的一项任务,田亮比李媛每小时多走1千米,结果比李媛早到半小时。设李媛每小时走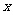 千米,依题意得到的方程是( )
千米,依题意得到的方程是( )
A. 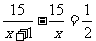 B.
B.
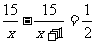
C.  D.
D.
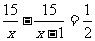
4. 方程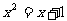 的根是( )
的根是( )
A. 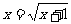 B.
B.

C. 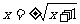 D.
D.
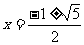
3. 下列四边形中,是轴对称图形,不是中心对称图形的是( )
A. 菱形 B. 矩形 C. 平行四边形 D. 等腰梯形
2. 如果 ,那么
,那么 的值为( )
的值为( )
A.  B.
B. 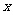 C.
C. 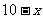 D.
D. 
1.  的值等于( )
的值等于( )
A. 1 B.  C.
C. 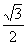 D.
D. 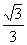
4、(2006山东济南)如图1,以矩形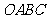 的两边
的两边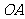 和
和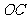 所在的直线为
所在的直线为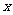 轴、
轴、 轴建立平面直角坐标系,
轴建立平面直角坐标系,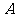 点的坐标为
点的坐标为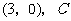 点的坐标为
点的坐标为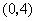 .将矩形
.将矩形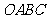 绕
绕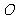 点逆时针旋转,使
点逆时针旋转,使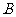 点落在
点落在 轴的正半轴上,旋转后的矩形为
轴的正半轴上,旋转后的矩形为 相交于点
相交于点 .
.
(1)求点 的坐标与线段
的坐标与线段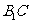 的长;
的长;
(2)将图1中的矩形 沿
沿 轴向上平移,如图2,矩形
轴向上平移,如图2,矩形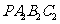 是平移过程中的某一位置,
是平移过程中的某一位置,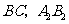 相交于点
相交于点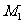 ,点
,点 运动到
运动到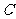 点停止.设点
点停止.设点 运动的距离为
运动的距离为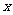 ,矩形
,矩形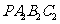 与原矩形
与原矩形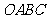 重叠部分的面积为
重叠部分的面积为 ,求
,求 关于
关于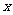 的函数关系式,并写出
的函数关系式,并写出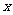 的取值范围;
的取值范围;
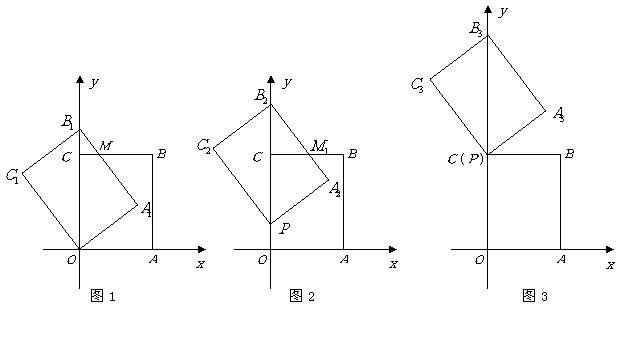 (3)如图3,当点
(3)如图3,当点 运动到点
运动到点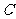 时,平移后的矩形为
时,平移后的矩形为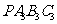 .请你思考如何通过图形变换使矩形
.请你思考如何通过图形变换使矩形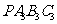 与原矩形
与原矩形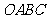 重合,请简述你的做法.
重合,请简述你的做法.
[解析]
(1)如图1,因为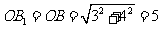 ,所以点
,所以点 的坐标为
的坐标为 .
.
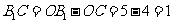 .
.
(2)在矩形 沿
沿 轴向上平移到
轴向上平移到 点与
点与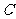 点重合的过程中,点
点重合的过程中,点 运动到矩形
运动到矩形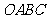 的边
的边 上时,求得
上时,求得 点移动的距离
点移动的距离 .
.
当自变量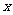 的取值范围为
的取值范围为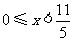 时,如图2,由
时,如图2,由 ,
,
得 ,此时,
,此时,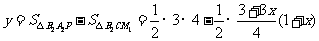 .
.
即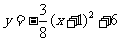 (或
(或 ).
).
当自变量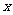 的取值范围为
的取值范围为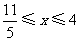 时,
时,
求得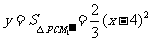 (或
(或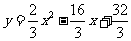 ).
).
3、(2006重庆)如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成 和
和 两个三角形(如图2所示).将纸片
两个三角形(如图2所示).将纸片 沿直线
沿直线 (AB)方向平移(点
(AB)方向平移(点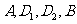 始终在同一直线上),当点
始终在同一直线上),当点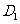 于点B重合时,停止平移.在平移过程中,
于点B重合时,停止平移.在平移过程中,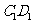 与
与 交于点E,
交于点E,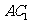 与
与 分别交于点F、P.
分别交于点F、P.
(1) 当 平移到如图3所示的位置时,猜想图中的
平移到如图3所示的位置时,猜想图中的 与
与 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;
(2) 设平移距离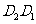 为
为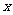 ,
, 与
与 重叠部分面积为
重叠部分面积为 ,请写出
,请写出 与
与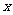 的函数关系式,以及自变量的取值范围;
的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的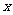 的值,使重叠部分的面积等于原
的值,使重叠部分的面积等于原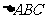 面积的
面积的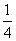 .
.
若存在,求x的值;若不存在,请说明理由.

[解析] (1)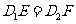 .因为
.因为 ,所以
,所以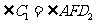 .
.
又因为 ,CD是斜边上的中线,
,CD是斜边上的中线,
所以,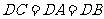 ,即
,即
所以,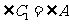 ,所以
,所以
所以,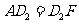 .同理:
.同理: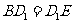 .
.
又因为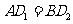 ,所以
,所以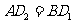 .所以
.所以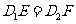
(2)因为在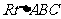 中,
中,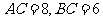 ,所以由勾股定理,得
,所以由勾股定理,得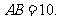
即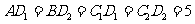
又因为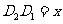 ,所以
,所以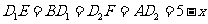 .所以
.所以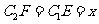
在 中,
中, 到
到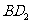 的距离就是
的距离就是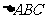 的
的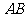 边上的高,为
边上的高,为 .
.
设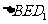 的
的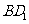 边上的高为
边上的高为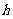 ,由探究,得
,由探究,得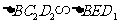 ,所以
,所以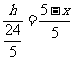 .
.
所以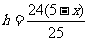 .
.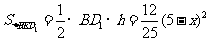
又因为 ,所以
,所以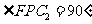 .
.
又因为 ,
,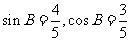 .
.
所以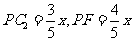 ,
,
而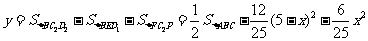
所以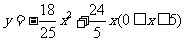
(3) 存在. 当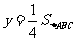 时,即
时,即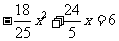
整理,得 解得,
解得, .
.
即当 或
或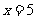 时,重叠部分的面积等于原
时,重叠部分的面积等于原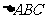 面积的
面积的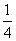 .
.
2、(2006河北)如图,在Rt△ABC中,∠C=90°,AC=12,BC=16,动点P从点A出发沿AC边向点C以每秒3个单位长的速度运动,动点Q从点C出发沿CB边向点B以每秒4个单位长的速度运动.P,Q分别从点A,C同时出发,当其中一点到达端点时,另一点也随之停止运动.在运动过程中,△PCQ关于直线PQ对称的图形是△PDQ.设运动时间为t(秒).
(1)设四边形PCQD的面积为y,求y与t的函数关系式;
(2)t为何值时,四边形PQBA是梯形?
(3)是否存在时刻t,使得PD∥AB?若存在,求出t的值;若不存在,请说明理由;
(4)通过观察、画图或折纸等方法,猜想是否存在时刻t,使得PD⊥AB?若存在,请估计t的值在括号中的哪个时间段内(0≤t≤1;1<t≤2;2<t≤3;3<t≤4);若不存在,请简要说明理由.
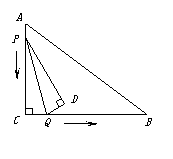 [解析] (1)由题意知
CQ=4t,PC=12-3t,
[解析] (1)由题意知
CQ=4t,PC=12-3t,
∴S△PCQ =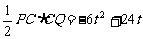 .
.
∵△PCQ与△PDQ关于直线PQ对称,
∴y=2S△PCQ 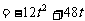 .
.
(2)当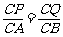 时,有PQ∥AB,而AP与BQ不平行,这时四边形PQBA是梯形,
时,有PQ∥AB,而AP与BQ不平行,这时四边形PQBA是梯形,
∵CA=12,CB=16,CQ=4t, CP=12-3t,
∴
 ,解得t=2.
,解得t=2.
∴当t=2秒时,四边形PQBA是梯形.
(3)设存在时刻t,使得PD∥AB,延长PD交BC于点M,如下图,
若PD∥AB,则∠QMD=∠B,又∵∠QDM=∠C=90°,
∴ Rt△QMD∽Rt△ABC,
Rt△QMD∽Rt△ABC,
从而 ,
,
∵QD=CQ=4t,AC=12,
AB=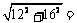 20,
20,
∴QM=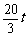 .
.
若PD∥AB,则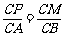 ,得
,得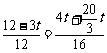 ,
,
解得t=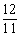 .
.
∴当t=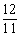 秒时,PD∥AB.
秒时,PD∥AB.
(4)存在时刻t,使得PD⊥AB.
时间段为:2<t≤3.
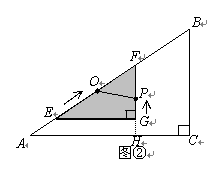
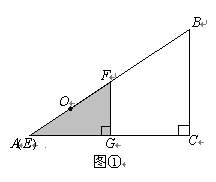
1、(2006山东青岛)如图①,有两个形状完全相同的直角三角形ABC和EFG叠放在一起(点A与点E重合),已知AC=8cm,BC=6cm,∠C=90°,EG=4cm,∠EGF=90°,O 是△EFG斜边上的中点.
如图②,若整个△EFG从图①的位置出发,以1cm/s 的速度沿射线AB方向平移,在△EFG 平移的同时,点P从△EFG的顶点G出发,以1cm/s 的速度在直角边GF上向点F运动,当点P到达点F时,点P停止运动,△EFG也随之停止平移.设运动时间为x(s),FG的延长线交 AC于H,四边形OAHP的面积为y(cm2)(不考虑点P与G、F重合的情况).
(1)当x为何值时,OP∥AC ?
(2)求y与x 之间的函数关系式,并确定自变量x的取值范围.
(3)是否存在某一时刻,使四边形OAHP面积与△ABC面积的比为13∶24?若存在,求出x的值;若不存在,说明理由.
(参考数据:1142 =12996,1152 =13225,1162 =13456
 或4.42 =19.36,4.52 =20.25,4.62 =21.16)
或4.42 =19.36,4.52 =20.25,4.62 =21.16)
[解析] (1)∵Rt△EFG∽Rt△ABC ,
∴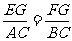 ,
,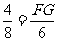 .
.
∴FG= =3cm.
=3cm.
∵当P为FG的中点时,OP∥EG ,EG∥AC ,
∴OP∥AC.
∴ x =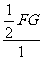 =
=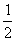 ×3=1.5(s).
×3=1.5(s).
∴当x为1.5s时,OP∥AC .
(2)在Rt△EFG 中,由勾股定理得:EF =5cm.
∵EG∥AH ,
∴△EFG∽△AFH .
∴ .
.
∴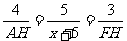 .
.
∴ AH= ( x +5),FH=
( x +5),FH=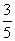 (x+5).
(x+5).
过点O作OD⊥FP ,垂足为 D .
∵点O为EF中点,
∴OD=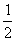 EG=2cm.
EG=2cm.
∵FP=3-x ,
∴S四边形OAHP =S△AFH -S△OFP
=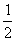 ·AH·FH-
·AH·FH-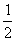 ·OD·FP
·OD·FP
=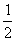 ·
· (x+5)·
(x+5)·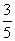 (x+5)-
(x+5)-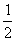 ×2×(3-x )
×2×(3-x )
=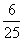 x2+
x2+ x+3
x+3
(0<x<3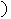 .
.
(3)假设存在某一时刻x,使得四边形OAHP面积与△ABC面积的比为13∶24.
则S四边形OAHP= ×S△ABC
×S△ABC
∴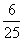 x2+
x2+ x+3=
x+3= ×
×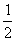 ×6×8
×6×8
∴6x2+85x-250=0
解得 x1=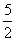 , x2= -
, x2= - (舍去).
(舍去).
∵0<x<3,
∴当x=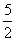 (s)时,四边形OAHP面积与△ABC面积的比为13∶24.
(s)时,四边形OAHP面积与△ABC面积的比为13∶24.
24. (本小题满分12分)
(本小题满分12分)
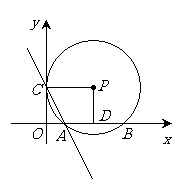
如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系. 以点P为圆心, PC为半径的⊙P与x轴的正半轴交于A、B两点, 若抛物线y=ax2+bx+4经过A, B, C三点, 且AB=6.
⑴求⊙P的半径R的长;
⑵求该抛物线的解析式并直接写出该抛物线与⊙P的第四个交点E的坐标;
⑶若以AB为直径的圆与直线AC的交点为F, 求AF的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com