
见作业纸
P77,1、2
补1.已知y与2x-1成反比例,且当x=1时,y=2,那么当x=0时,y=________.
2. 若函数y=(m-1)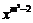 是反比例函数,则m的值等于( )
是反比例函数,则m的值等于( )
A.±1 B.1 C.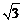 D.-1
D.-1
例1下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?
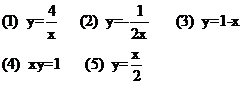
例2 已知变量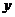 与
与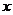 成反比例,当
成反比例,当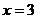 时,
时,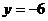 .
.
求(1)y与x之间的函数关系式;(2)当 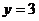 时,
时,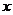 的值
的值
例3 已知y-2与x成反比例,且当x=2时,y=4,求y与x之间的函数关系式.
3.反比例函数的概念
一般地,如果两个变量x, y之间的关系可以表示成 y=(k为常数,k≠0)的形式,那么称y是x的反比例函数.k是比例系数.
反比例函数的自变量x 不能为零.
2.上面的函数关系式具有什么共同的特征?你还能举出类似的实例吗?
1.做一做
用函数关系式表示下列问题中的两个变量之间的关系.
(1) 一个面积为6400cm2的长方形的长a(m)随宽b(m)的变化而变化.
(2)某银行为资助某社会福利厂,提供了20万元的无息贷款,该厂的平均年还款额y(万元)随还款年限x(年)的变化而变化.
(3)游泳池的容积为5000 m3向池内注水,注满水所需时间t(h)随注水速度
v(m3/h) 的变化而变化.
(4)实数m与n的积为-200,m随n的变化而变化.
3.U=IR,当U=220V时,
(1)你能用含R的代数式表示I吗?
(2)利用写出的关系式完成下表:
|
R(Ω) |
20 |
40 |
60 |
80 |
100 |
|
I(A) |
|
|
|
|
|
当R越来越大时,I怎样变化?
当R越来越小呢?
(3)变量I是R的函数吗?为什么?
2.汽车从南京出发开往上海(全程约300km),全程所用时间t(h)随速度v(km/h)的变化而变化.
(1)你能用含有v的代数式表示t吗?
(2)利用(1)的关系式完成下表.
|
v(km/h) |
60 |
80 |
90 |
100 |
120 |
|
t(h) |
|
|
|
|
|
随着速度的变化.全程所用的时间发生怎样的变化?
(3)速度v是时间t的函数吗?为什么?
1.从现实情况和已有知识经验出发,讨论两个变量之间的相依关系,加强对函数概念的理解,导入反比例函数.
2、已知y-3与x+2 成反比例,且x=2时,y=7,求(1)y与x的函数关系式.(2)求y=5时,x的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com