19．1．2平行四边形的性质及判定阶段小测验

检测内容：平行四边形的性质及判定。

检测时间：一课时。

评讲平行四边形的性质及判定阶段小测验

教学时间：一课时。

练习册。

19．1．2平行四边形的判定(五)

讲评平行四边形部分的练习册内容。

我们通过用学过的平行四边形的判定及性质证明三角形中位线定理，并且学会将三角形转化为平行四边形解决问题，学会添加辅助线的一些方法。

引入：让学生回顾课本P98的“思考”。

例题讲解：课本P4。

提示：能否将三角形的问题转化为平行四边形的问题来解决呢？

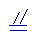
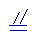分析：由点E是三角形AC边的中点，再延长DE使线段EF的长等于线段DE的长，将四个端点连结起来，得到一个对角线互相平分的四边，即得到一个平行四边形。可得线段CF　 DA，可行CF　 BD，得到四边形BDFC也是一个平行四边形，可得DF=BC，因此得到DF∥BC，且DF=BC，又。

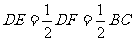板书证明过程。

小结：三角形中位线：

前提：三角形二边的中点连线这条线段；

结论：该线段与三角形的第三边平行，并且等于第三边的一半。

几何语言表达：

∵AD=CD AE=BE

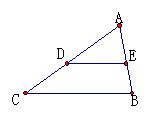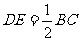∴，DE ∥BC

练习：课本练习题第1、3题(提问)

练习册。(用其中二道题当堂让学生板书)

2．判定一个四边形是平行四边形有哪些方法？

1．平行四边形有哪些性质？

3．掌握三角形与平行四边形的相互转化，学会用添辅助线。

教学重点：

应用平行四边形的性质和判定得出三角形的中位线性质。

教学难点：

会用添加辅助线，将三角形与平行四边形之间的合理转化。

教学用具：投影仪、尺等。

教学时间 ：一课时。

教学过程：

2．掌握三角形中位线的性质，并能应用来解决实际问题。

1．能应用平行四边形的性质及判定方法来证明实际问题。

19．1．2平行四边形的判定(四)

教学目的：