
1. 若代数式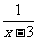 在实数范围内有意义,则
在实数范围内有意义,则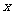 的取值范围为(※)
的取值范围为(※)
(A) 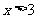 (B)
(B)
 (C)
(C)  (D)
(D)
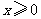 且
且
24.(本小题满分14分)如图,在直角坐标系中,⊙A的半径为4,A的坐标为(2,0),
⊙A与x轴交于E、F两点,与y轴交于C、D两点,过C点作⊙A的切线BC交x轴于B.
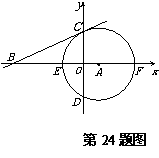 (1)求直线BC的解析式;(4分)
(1)求直线BC的解析式;(4分)
(2)若一抛物线与x轴的交点恰为⊙A与x轴的两个交点,且抛物线的顶点在直
线上y=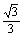 x+2
x+2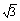 上,求此抛物线的解析式;(8分)
上,求此抛物线的解析式;(8分)
(3)试判断点C是否在抛物线上,并说明理由(2分)
21.(本题满分10分) 已知关于x的不等式ax+3>0(其中a≠0).
(1)当a=-2时,求此不等式的解,并在数轴上表示此不等式的解集;(4分)
(2)小明准备了十张形状、大小完全相同的不透明卡片,上面分别写有整数-10、-9、-8、-7、-6、-5、-4、-3、-2、-1,将这10张卡片写有整数的一面向下放在桌面上.从中任意抽取一张,以卡片上的数作为不等式中的系数a,求使该不等式没有正整数解的概率.(6分)
22(本题满分10分)为了落实国务院副总理李克强同志到恩施考察时的指示精神,最近,州委州政府又出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w(千克)与销售价x(元/千克)有如下关系:w=-2x+80.设这种产品每天的销售利润为y(元).
(1)求y与x之间的函数关系式.
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?
20.(本题满分8分)如图, 是⊙
是⊙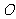 的直径,点
的直径,点 是半径
是半径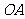 的中点,点
的中点,点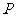 在线段
在线段 上运动(不与点
上运动(不与点 重合).点
重合).点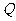 在上半圆上运动,且总保持
在上半圆上运动,且总保持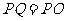 ,过点
,过点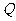 作⊙
作⊙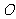 的切线交
的切线交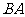 的延长线于点
的延长线于点
(1)当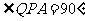 时,判断
时,判断 是
三角形;(2分)
是
三角形;(2分)
(2)当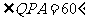 时,请你对
时,请你对 的形状做出猜想,并给予证明;(4分)
的形状做出猜想,并给予证明;(4分)
(3)由(1)、(2)得出的结论,进一步猜想,当点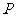 在线段
在线段 上运动到任何位置时,
上运动到任何位置时, 一定是
三角形。(2分)
一定是
三角形。(2分)
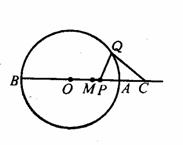
18.  (本题满分8分)如图,
(本题满分8分)如图, 内接于
内接于 ,
, 为
为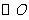 的直径,
的直径,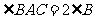 ,
,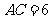 ,过点
,过点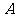 作
作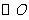 的切线与
的切线与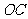 的延长线交于点
的延长线交于点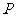 ,求
,求 的长
的长
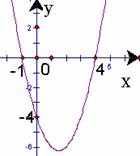 19(本题满分8分)已知二次函数
19(本题满分8分)已知二次函数 的图象如图:
的图象如图:
①对称轴方程是:__________;(2分)
②点 是图象上的两个点,且
是图象上的两个点,且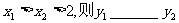 (2分)
(2分)
③求函数解析式(4分)
17.计算题(本题2小题,每题6分,共12分)
(1)当x取何值时,代数式2x2-3x+6与代数式x2+10值相同?
(2)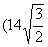 -
-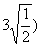 -(
-(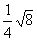 -
-
16. 六个面上分别标有1,1,2,3,3,5六个数字的均匀六方体表面如图所示,掷这个
六方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数
|
|
3 |
|
|
|
3 |
|
|
|
2 |
|
|
1 |
5 |
1 |
为该点的纵坐标。按照这样的规定,每掷一次该六方体,就能得到平面内的一个点的坐标。已知小明前两次掷得的两个点能确定一条直线 ,且这条直线
,且这条直线 经过点
经过点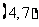 。
。
那么,他第三次掷得的点也在这条直线上的概率是----
15.设抛物线的解析式是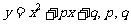 为常数,且
为常数,且 对于
对于 ,其函数值
,其函数值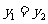 ,则当
,则当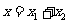 时的函数值是----
时的函数值是----
14. 如图,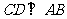 于
于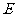 ,若
,若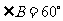 ,则
,则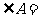 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com