
24.(本小题满分14分)
 如图12,
如图12, 、
、 为
为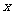 轴上的两点,以
轴上的两点,以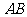 为直径的半圆交
为直径的半圆交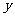 轴的正半轴于点
轴的正半轴于点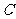 .
.
(1)求点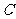 的坐标;
的坐标;
(2)求经过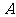 、
、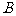 、
、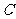 三点的抛物线的解析式,
三点的抛物线的解析式,
并写出抛物线的顶点坐标和对称轴方程;
(3)在抛物线上是否存在点 ,使
,使 ≌
≌ ?
?
若存在,试求出所有符合条件的点的坐标;若不存在,说明理由.
解:(1)
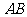 为⊙
为⊙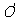 的直径,
的直径,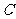 为⊙
为⊙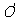 上的异于
上的异于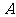 、
、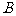 点,
点, ,…(1分)
,…(1分)
 ,又
,又 ,
,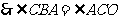 .
.
 ∽
∽ . …………………………………………………………(3分)
. …………………………………………………………(3分)
 .即
.即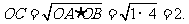 ……………………………………(4分)
……………………………………(4分)
(2)由题意设抛物线的解析式为 , ………………………………(5分)
, ………………………………(5分)
则由抛物线过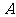 、
、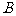 有:
有: ………………………………(7分)
………………………………(7分)
解这个方程组得: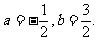
故所求抛物线的解析式为 ………………………………(8分)
………………………………(8分)
顶点坐标为 , 对称轴
, 对称轴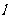 的方程为
的方程为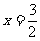 ………………………………(10分)
………………………………(10分)
(3)存在点 ,使
,使 ≌
≌ .
…………………………………………(11分)
.
…………………………………………(11分)
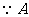 、
、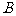 关于抛物线的对称轴
关于抛物线的对称轴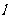 对称,
对称, 点
点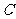 关于对称轴
关于对称轴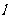 对称的点
对称的点 既在抛物线上,也在以
既在抛物线上,也在以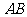 为直径的⊙
为直径的⊙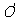 上,即
上,即 且
且 ≌
≌ .……(13分)
.……(13分)
要使抛物线上的 点满足
点满足 ≌
≌ ,必须
,必须 ,即
,即 为⊙
为⊙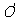 与抛物线的交点,而异于
与抛物线的交点,而异于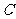 的交点只有一个,故点
的交点只有一个,故点 是唯一存在的点.…………(14分)
是唯一存在的点.…………(14分)
[说明:若末收到 更正为
更正为 的通知,学生回答“不存在点
的通知,学生回答“不存在点 ,使
,使 ≌
≌ ”也可以酌情给分,但给满分必须是利用对称性来排除,并且说理清晰,否则扣一分]
”也可以酌情给分,但给满分必须是利用对称性来排除,并且说理清晰,否则扣一分]
23.解:(1)由题意有: ,
,
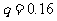 . …………(2分)
. …………(2分)
又
 ,
, 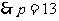 .
………………(4分)
.
………………(4分)
补充统计图如图所示(图略). ……………………………………………(7分)
(2)在80.5-90.5的分数组内 …………………………………………(9分)
(3)能获奖的概率为0.3 0.26
0.26 0.56 .
…………………………………………(12分)
0.56 .
…………………………………………(12分)
23.(本小题满分12)
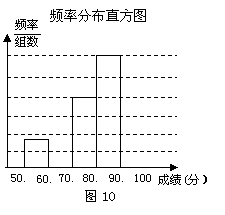 青少年宫为了让中学生了解环保知识,增强环保意识,举办了一次中学生环保知识竞赛,共有1200名学生参加这次竞赛.为了解本次竞赛的情况,从中抽取了部分学生的成绩(分值均为正整数,满分为100分)进行统计分析.
青少年宫为了让中学生了解环保知识,增强环保意识,举办了一次中学生环保知识竞赛,共有1200名学生参加这次竞赛.为了解本次竞赛的情况,从中抽取了部分学生的成绩(分值均为正整数,满分为100分)进行统计分析.
|
分组 |
频数 |
频率 |
|
50.5-60.5 |
4 |
0.08 |
|
60.5-70.5 |
8 |
 |
|
70.5-80.5 |
10 |
0.20 |
|
80.5-90.5 |
15 |
0.30 |
|
90.5-100 |
 |
0.26 |
|
合计 |
|
|
频率分布表
请根据上述统计图表,解答下列问题:
(1)试求频率分布表中 、
、 的值,补全频率分布直方图;
的值,补全频率分布直方图;
(2)在全体参赛学生中,竞赛成绩的中位数落在哪个组内?
(3)若成绩在80分以上(不含80分)可以获奖,在参赛学生的试卷中随机取一张,能获奖的概率有多大?
22.解:(1)
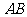 为⊙
为⊙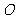 的直径,
的直径,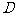 为⊙
为⊙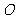 上异于
上异于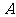 、
、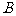 的点,
的点,
 ,即
,即 …………………………………………(1分)
…………………………………………(1分)
由勾股定理可得 .
…………………………………………(2分)
.
…………………………………………(2分)
 .
…………………………………………(3分)
.
…………………………………………(3分)
 又
又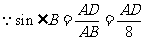 ,
, 得
得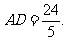 …………………………(4分)
…………………………(4分)
(2) .
………………………(5分)
.
………………………(5分)
设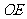 与
与 交于点
交于点 ,
,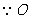 ,
, 分别为
分别为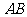 、
、 的中点,
的中点,
 ,
………………………(7分)
,
………………………(7分)
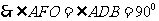 ,
, 
 .……………(8分)
.……………(8分)
(3)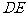 是⊙
是⊙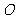 的切线(
的切线(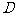 为切点). ……………(9分)
为切点). ……………(9分)
由(2)知 ,
, ,
,  ,即
,即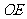 垂直平分
垂直平分 .
.
 四边形
四边形 关于
关于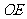 成轴对称图形,
成轴对称图形, ,
,
即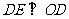 ,而
,而 为⊙
为⊙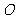 的半径,
的半径,  是⊙
是⊙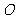 的切线. …………………(11分)
的切线. …………………(11分)
 .
.
即切线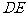 的长为
的长为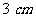 . …………………………………………………(12分)
. …………………………………………………(12分)
22.(本小题满分12分)
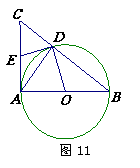 如图11,以
如图11,以
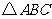 的边
的边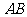 为直径的⊙
为直径的⊙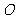 交边
交边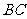 于点
于点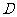 ,
, 为
为 的中点,且
的中点,且 ,
,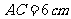 .
.
(1)求 的长和
的长和 的值;
的值;
(2)连结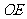 ,判断
,判断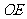 与
与 是否垂直?为什么?
是否垂直?为什么?
(3)判断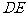 是否是⊙
是否是⊙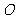 的切线?若是,试求出切
的切线?若是,试求出切
线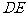 的长;若不是,请说明理由;
的长;若不是,请说明理由;
21. 解:(1)参加第一场比赛的有
解:(1)参加第一场比赛的有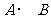 、
、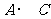 、
、 三种情况,
三种情况, 队被确定参加第一场比赛的概率为
队被确定参加第一场比赛的概率为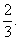 ………………(3分)
………………(3分)
(2)三队队长第一回合 “抛硬币”结果
可用树状图表示如图,抛硬币共有8种结
果,其中“正-正-正”、“反-反-反”
两种,故第一个回合不能确定出比赛两队的
概率为: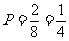 . ……………………………………………(9分,其中树状图给3分)
. ……………………………………………(9分,其中树状图给3分)
(3)略(示例:抛三枚同币值硬币,规则类同). ………………………………………(12分)
[评分说明:若考生在(1)中误用了(2)的树状图,若树状图正确仍给树状图的3分]
21.(本小题满分12分)
某校9年级有A、B、C三个排球队,准备在“五一”期间进行友谊比赛,为了确定哪两个球队进行第一场比赛,他们约定用“抛硬币”的方式来确定: 三个球队的队长在水平地面上抛同一枚质地均匀的硬币,各抛一次为一个回合.在一个回合中,若恰有两次币面相同(正面向上或者反面向上),则抛出相同币面的两队先行比赛;若三次都正面向上或者反面向上,则再来一个回合,直至确定先进行比赛的两支球队为止.
(1)求C队被确定参加第一场比赛的概率;
(2)求第一个回合不能确定出比赛两队的概率,并用树状图加以说明.
(3)仍然以“硬币”为工具,再设计一种公平的确定出两队先进行比赛的方式.
20.解:(1)依题意得,直线 的解析式为
的解析式为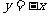 .… (3分)
.… (3分)
因为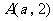 在直线
在直线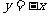 上, 则
上, 则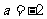 .…(5分)
.…(5分)
即得 .
.
又因为 在
在 的图象上,
的图象上,
 ,得
,得 .……………………………………………………(6分)
.……………………………………………………(6分)
所以反比例函数的解析式为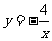 .……………………………………(7分)
.……………………………………(7分)
作图(图略) ………………………………………………………………(10分)
20.(本小题满分10分)
 在平面直角坐标系
在平面直角坐标系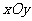 中,直线
中,直线 绕点
绕点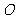 顺时针旋转
顺时针旋转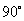 得到直线
得到直线 .又直线
.又直线 与反比例函数
与反比例函数 的图象的一个交点为
的图象的一个交点为 .
.
(1)求直线 的方程.
的方程.
(2)求反比例函数的解析式,并作出它的大致图象.
19.(1)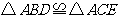 、
、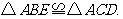 …(4分)
…(4分)
(2)证明: ,
,
 , ………………… (6分)
, ………………… (6分)
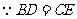 ,
,
 , ……………… (8分)
, ……………… (8分)
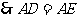 .
………………… (9分)
.
………………… (9分)
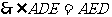 …………………… (10分)
…………………… (10分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com