26．(8分)已知，如图8，AB和DE是直立在地面上的两根立柱.AB=5m，某一时刻AB在阳光下的投影BC=3m，

(1)请你在图8中画出此时DE在阳光下的投影；

(2)在测量AB的投影时，同时测量出DE在阳光下的投影长为6m，请你计算DE的长.

25．(6分)为了测量校园内一棵不可攀的树的高度，学校数学应用实践小组做了如下的探索：

实践：根据《自然科学》中的反射定律，利用一面镜子和一根皮尺，设计如右示意图的测量方案：把镜子放在离树(AB)8.7米的点E处，然后沿着直线BE后退到点D，这是恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.7米，观察者目高CD=1.6米，请你计算树(AB)的高度．(精确到0.1米)

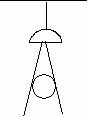
24．(6分)如图，在一间黑屋里用一白炽灯照射一个球，

(1)球在地面上的阴影是什么形状？

(2)当把白炽灯向上移时，阴影的大小会怎样变化？

(3)若白炽灯到球心距离为1米，到地面的距离是 3米，球的半径是0.2米，求球在地面上阴影的面积是多少？

23．(6分)中午，一根1.5米长的木杆影长1.0米，一座高21米的住宅楼的影子是否会落在相距18米远的商业楼上？傍晚，该木杆的影子长为2.0米，这时住宅楼的影子是否会落在商业楼上？为什么？

22．(6分)李栓身高1. 88 m ，王鹏身高1.60 m ，他们在同一时刻站在阳光下，李栓的影子长为1.20 m ，求王鹏的影长。

21．(4分)立体图形的三视图如下，请你画出它的立体图形：

20．(4分)画出下面实物的三视图：

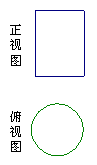
19．(4分)一个物体的正视图、俯视图如图所示，请你画出该物体的左视图并说出该物体形状的名称。

18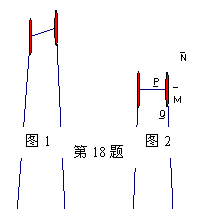．如图1表示正六棱柱形状的高大建筑物，图2中的阴影部分表示该建筑物的俯视图，P、Q、m、n表示小明在地面上的活动区域，小明想同时看到该建筑物的三个侧面，他应在　　　　　　　　　 (　　 )

A．P区域　 B．Q区域　 C．m区域　 D．n区域

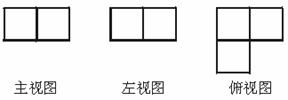
17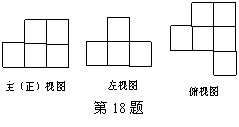．右图是由一些完全相同的小立方块搭成的几何体的三种视图，那么搭成这个几何体所用的小立方块的个数是　　 (　 )

A．5个　　　　 B．6个　　　　　

C．7个　　　　 D．8个