
30. (12分)如图12,已知二次函数图象的顶点坐标为C(1,0),直线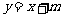 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴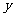 上.
上.
(1)求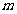 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作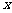 轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为
轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为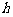 ,点P的横坐标为
,点P的横坐标为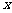 ,求
,求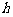 与
与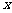 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量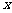 的取值范围;
的取值范围;
 (3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
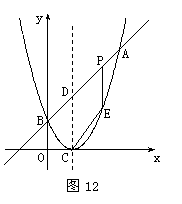
29.(9分)某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的200天内,西红柿市场售价与上市时间的关系,用图①的一条线段来表示;西红柿的种植成本与上市时间的关系,用图②中的一段抛物线表示.
(1)写出图①表示的市场售价与时间的函数关系式y1=kt+m;写出图②表示的种植成本与时间的函数关系式y2=at2+bt+c.
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价和种植成本的单位:元/10km,时间单位:天)
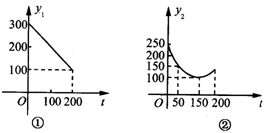
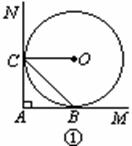
27.(11分)(1)如图①,直线AM⊥AN, ⊙O分别与AM、AN相切于B、C两点,连结OC、BC,证明∠ACB=∠OCB
(2)将图①中直线AN向右平移,与⊙O相交于C1、C2两点,⊙O与AM的切点仍记为B,如图②.请你写出与平移前相应的结论,并将图②补充完整;判断此结论是否成立,且说明理由.
26. (6分)一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会可能地向左或向右落下。试问小球通过第二层A位置的概率是多少?第三层B位置的概率是多少?
(6分)一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会可能地向左或向右落下。试问小球通过第二层A位置的概率是多少?第三层B位置的概率是多少?
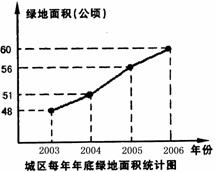
25.(7分)美化城市,改善人们的居住环境已成为城市建设的一项重要内容.某市城区近几年来,通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加(如图所示)
(1)根据图中所提供的信息,回答下列问题:2006年底的绿地面积为 公顷,比2005年底增加了 公顷;在2004年,2005年,2006年这三年中, 绿地面积增加最多的是 年;
(2)为满足城市发展的需要,计划到2008年底使城区绿地总面积达到72.6公顷,试求今明两年绿地面积的年平均增长率.
24.如图,D是⊿ABC的边AB上一点,在下列条件中,一定使⊿ABC∽⊿ACD的是( )
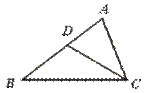
A.△ACD=∠B B.AC2=AD·AB,
C.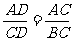 D.∠B=∠ACB
D.∠B=∠ACB
23.已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=-1,与x轴的一个交点为(x1,0),且0<x1<1,下列结论中正确结论的是( )
A.9a-3b+c>0 B. b<a; C.3a+c>0 D.b=-2a
22、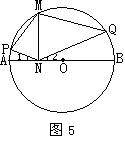 如图,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N,P、Q分别是AM、BM上一点(不与端点重合),如果∠MNP=∠MNQ,下面结论正确的是( )
如图,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N,P、Q分别是AM、BM上一点(不与端点重合),如果∠MNP=∠MNQ,下面结论正确的是( )
A.∠1=∠2 B.∠P+∠Q=∠180°
C.∠Q=∠PMN D.PM=QM E.MN2=PN·QN。
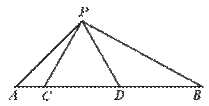
21.(6分)如图,点C、D在线段AB上,⊿PCD是等边三角形.
(1)当AC、CD、DB满足怎样的关系时,⊿ACP∽⊿PDB?
(2)当⊿ACP∽⊿PDB时,求⊿APB的度数.
20.(3分)
(1)计算: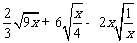
(2)(3分)解方程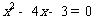
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com