
1. 三角形的三边长分别为6,8,10,它的最短边上的高为( )
A. 6 B. 4.5 C. 2.4 D. 8
7.已知y=y1+y2, y1与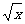 成正比例,y2与x2成反比例.当x=1时,y=-12;当x=4时,y=7.(1)求y与x的函数关系式和x的取范围;(2)当x=
成正比例,y2与x2成反比例.当x=1时,y=-12;当x=4时,y=7.(1)求y与x的函数关系式和x的取范围;(2)当x=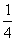 时,求y的值(6)
时,求y的值(6)
.
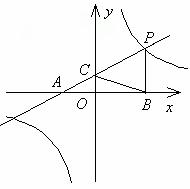 8如图,点P是直线
8如图,点P是直线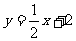 与双曲线
与双曲线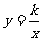 在第一象限内的一个交点,直线
在第一象限内的一个交点,直线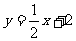 与x轴、y轴的交点分别为A、C,过P作PB垂直于x轴,若AB+PB=9.
与x轴、y轴的交点分别为A、C,过P作PB垂直于x轴,若AB+PB=9.
(1)求k的值;(2)求△PBC的面积.(6)
1.一定质量的二氧化碳,当它的体积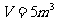 时,它的密度
时,它的密度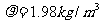 .①求
.①求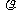 与V的函数关系式;②当
与V的函数关系式;②当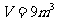 时,求二氧化碳的密度
时,求二氧化碳的密度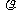 .(4)
.(4)
 2(7)如图正比例函数y=k1x与反比例函数
2(7)如图正比例函数y=k1x与反比例函数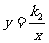 交于点A,从A向x轴、y轴分别作垂线,所构成的正方形的面积为4。
交于点A,从A向x轴、y轴分别作垂线,所构成的正方形的面积为4。
①分别求出正比例函数与反比例函数的解析式。
②求出正、反比例函数图像的另外一个交点坐标。
③求△ODC的面积。
.
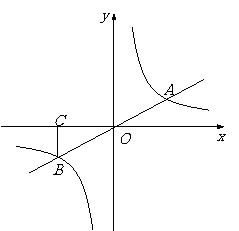
3(7)
如图,正比例函数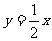 与反比例函数
与反比例函数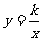 的图象相交于
的图象相交于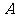 、
、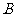 两点,过
两点,过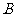 作
作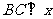 轴,垂足为
轴,垂足为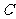 ,且△
,且△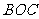 的面积等于4.
的面积等于4.
(1)求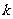 的值;(2)求
的值;(2)求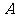 、
、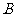 两点的坐标;
两点的坐标;
 (3)在
(3)在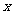 轴的正半轴上是否存在一点
轴的正半轴上是否存在一点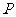 ,使得△
,使得△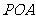 为直角三角形?若存在,请求出点
为直角三角形?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
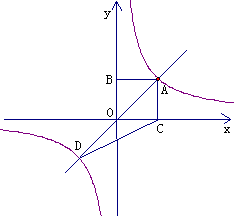
4{7}如图13-8-7已知一次函数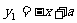 与x轴、y轴分别交于
与x轴、y轴分别交于
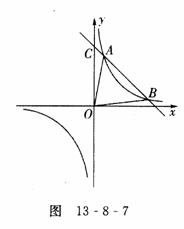 点D、C两点和反比例函数
点D、C两点和反比例函数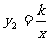 交于A、B两点,且点A的
交于A、B两点,且点A的
坐标是(1,3)点B的坐标是(3,m)求a,k,m的值;
(1) 求C、D两点的坐标,并求△AOB的面积;
(2) 利用图像直接写出,当x在什么取值范围时,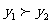 ?
?
5(7)某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
|
日销售单价x(元) |
3 |
4 |
5 |
6 |
|
日销售量y(个) |
20 |
15 |
12 |
10 |
(1)猜测并确定y与x之间的函数关系式;
(2)设经营此贺卡的销售利润为W元,求出W与x之间的函数关系式.若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价x定为多少时,才能获得最大日销售利润?
6(8).已知反比例函数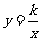 的图像与一次函数y=kx+m的图像相交于点A(2,1).
的图像与一次函数y=kx+m的图像相交于点A(2,1).
(1)分别求出这两个函数的解析式;
(2)当x取什么范围时,反比例函数值大于0;
 (3)若一次函数与反比例函数另一交点为B,且纵坐标为-4,当x取什么范围时,反比例函数值大于一次函数的值;
(3)若一次函数与反比例函数另一交点为B,且纵坐标为-4,当x取什么范围时,反比例函数值大于一次函数的值;
(4)试判断点P(-1,5)关于x轴的对称点P‘是否在一次函数y=kx+m的图像上.
7.已知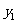 +
+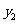 =y,其中
=y,其中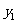 与
与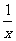 成反比例,且比例系数为
成反比例,且比例系数为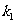 ,而
,而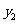 与
与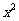 成正比例,且比例系数为
成正比例,且比例系数为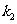 ,若x=-1时,y=0,则
,若x=-1时,y=0,则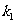 ,
,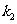 的关系是( )
的关系是( )
A.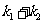 =0
B.
=0
B.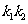 =1 C.
=1 C.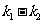 =0
D.
=0
D.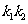 =-1
=-1
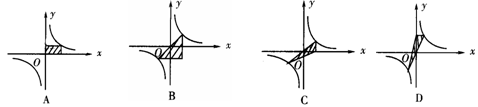
6. 在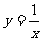 的图象中,阴影部分面积不为
的图象中,阴影部分面积不为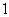 的是( ).
的是( ).
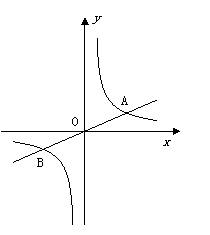
5.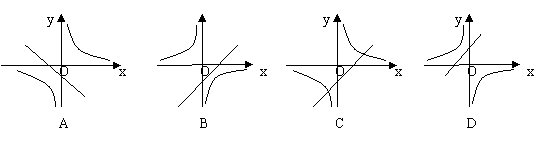 如图,关于x的函数y=k(x-1)和y=-
如图,关于x的函数y=k(x-1)和y=-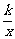 (k≠0), 它们在同一坐标系内的图象大致是( )
(k≠0), 它们在同一坐标系内的图象大致是( )
3.面积为4的矩形一边为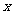 ,另一边为y,则y与x的变化规律用图象大致表示为 ( )
,另一边为y,则y与x的变化规律用图象大致表示为 ( )
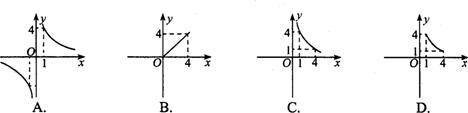
4下列各点中,在函数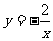 的图像上的是( )
的图像上的是( )
A、(2,1) B、(-2,1) C、(2,-2) D、(1,2)
2.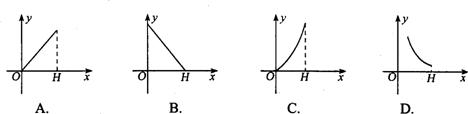 向高为H的圆柱形水杯中注水,已知水杯底面半径为2,那么注水量y与水深x的函数图象是 ( )
向高为H的圆柱形水杯中注水,已知水杯底面半径为2,那么注水量y与水深x的函数图象是 ( )
1、 函数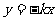 与
与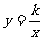 (
(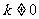 )的图象的交点个数是( )
)的图象的交点个数是( )
A. 0 B. 1 C. 2 D. 不确定
21.(14分)(福州)如图,已知直线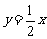 与双曲线
与双曲线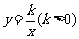 交于点A,B两点,且点A的横坐标为4.
交于点A,B两点,且点A的横坐标为4.
(1)求k的值;
(2)若双曲线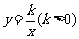 上一点C的纵坐标为8,求△AOC的面积;
上一点C的纵坐标为8,求△AOC的面积;
(3)过原点O的另一条直线l交双曲线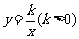 于P、Q两点(P在第一象限),若由点A、B、P、Q为顶点的四边形面积为24,求点P的坐标.
于P、Q两点(P在第一象限),若由点A、B、P、Q为顶点的四边形面积为24,求点P的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com