8、一个正方形在平面直角坐标系中三个顶点的坐标为(－2，－3)，(－2，1)，(2，1)，则第四个顶点的坐标为(　　 )

　 A、(2，2)　　　　 B、(3，2)　　　　 C、(2，－3)　　　　　 D、(2，3)

7、若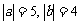，且点M(a，b)在第二象限，则点M的坐标是(　　 )

　 A、(5，4)　　　 B、(－5，4)　　 　C、(－5，－4)　　　 D、(5，－4)

6、如果点A(m，n)的坐标满足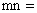0，则点A在(　　 )

　 A、原点上　　　　 B、坐标轴上　　　　 C、x轴上　　　　　 D、y轴上

5、若点P(a，b)在第三象限，则点P₁(－a，－b)在(　　　 )

　 A、第一象限　　　 B、第二象限　　　 C、第三象限　　　　 D、第四象限

4、要确定珠穆朗玛峰在地球仪上的位置，需要知道它在地球仪上的(　　 )

　 A、高度　　　　 B、经度　　　　 C、纬度　　　　　 D、经度和纬度

3、若y轴上的点P到x轴的距离为3，则点P的坐标为(　　 )

　 A、(3，0)　 B、(0，3)　　 C、(3，0)或(－3，0)　　 D、(0，3)或(0，－3)

2、平行于x轴的直线上的任意两点的坐标之间的关系是(　　 )

A、横坐标相等　　　　　　 　　　B、纵坐标相等

C、横坐标的绝对值相等　　　　　 D、纵坐标的绝对值相等

1、如图是在方格纸上画出的小旗图案，若用(0，0)表示A点，　

(0，4)表示B点，那么C点的位置可表示为(　　 )

A、(0，3)　　 B、(2，3)　　 C、(3，2)　　 D、(3，0)

2．探索活动

　　 情境设计和探索活动，可以从两方面体现“问题是数学的心脏”这一推动数学发生、发展的重要理念：

由问题引导复习活动展开；以实际问题为中心构建本章知识网络．例如：

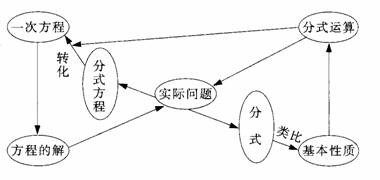
　　 此外，在“分式概念”单元复习时，注意引入课本“小结与思考”中分式、整式和有理式间的关系；在“分式方程”单元复习时，注意引入课本“小结与思考”中求解的一般步骤．强化“类比”与“转化”的数学思想方法的应用．

1．情境创设

　　 可将学生在数学活动中出现的错误作为问题情境，展开复习小结．也可以直接设计问题串，让学生举例，展开复习．例如：

　　 (1)本章学习了哪些知识?指导全章探索活动的主要思想方法是什么?

　　 (2)什么是分式?分式与分数有什么区别与联系?你能举例说明吗?

　　 (3)分式与分数的基本性质相同吗?你能举例说明吗?

　　 (4)举例说明分式的约分、通分与分数的约分、通分有什么相同和不同之处?

　　 (5)能举例说明解分式方程的基本步骤吗?