
1、下列词语中加点字读音正确的一组是:
A.漱(shù)口 龋(yǔ)齿 浣(huàn)纱 否(pǐ)极泰来
B.孵(fū)化 铺(pù)板 碑帖(tiě) 色厉内荏(rěn)
C.平仄(zè) 哨卡(kǎ) 彳亍(chù) 胼手胝(zhī)足
D.压轴(zhòu)戏 囹圄(yǔ) 垄(lǒng)沟 涎(xián)皮赖脸
3. 若
若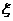 的分布列为:
的分布列为:
|
x |
0 |
1 |
|
P |
p |
q |
其中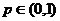 ,则
,则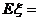 ____________________,
____________________,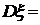 ____________________,
____________________,
2. 设某项试验的成功概率是失败概率的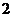 倍,用随机变量
倍,用随机变量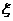 描述
描述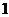 次试验的成功次数,
次试验的成功次数,
则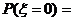 _______________。
_______________。
1. 抛掷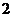 颗骰子,所得点数之和记为
颗骰子,所得点数之和记为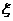 ,那么
,那么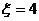 表示的随机试验结果为____________。
表示的随机试验结果为____________。
12.袋中有大小相同的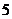 个白球和
个白球和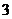 个黑球,从中任意摸出
个黑球,从中任意摸出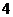 个,求下列事件发生的概率.
个,求下列事件发生的概率.
(1)摸出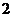 个或
个或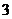 个白球 (2)至少摸出一个黑球.
个白球 (2)至少摸出一个黑球.
解: (Ⅰ)设摸出的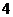 个球中有
个球中有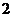 个白球、
个白球、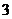 个白球分别为事件
个白球分别为事件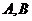 ,则
,则
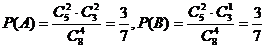
∵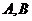 为两个互斥事件
∴
为两个互斥事件
∴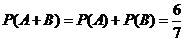
即摸出的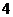 个球中有
个球中有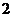 个或
个或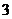 个白球的概率为
个白球的概率为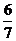
(Ⅱ)设摸出的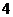 个球中全是白球为事件
个球中全是白球为事件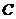 ,则
,则
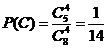 至少摸出一个黑球为事件
至少摸出一个黑球为事件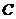 的对立事件
的对立事件
其概率为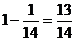
练习:
11.高三(1)班、高三(2)班每班已选出3名学生组成代表队,进行乒乓球对抗赛. 比赛规则是:①按“单打、双打、单打”顺序进行三盘比赛;
②代表队中每名队员至少参加一盘比赛,不得参加两盘单打比赛. 已知每盘比赛双方胜出的概率均为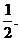
(Ⅰ)根据比赛规则,高三(1)班代表队共可排出多少种不同的出场阵容?
(Ⅱ)高三(1)班代表队连胜两盘的概率是多少?
解:(I)参加单打的队员有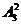 种方法.
种方法.
参加双打的队员有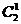 种方法.
种方法.
所以,高三(1)班出场阵容共有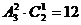 (种)
(种)
(II)高三(1)班代表队连胜两盘,可分为第一盘、第二盘胜或第一盘负,其余两盘胜,
所以,连胜两盘的概率为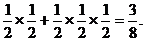
10.有一批食品出厂前要进行五项指标检验,如果有两项指标不合格,则这批食品不能出厂.已知每项指标抽检是相互独立的,且每项抽检出现不合格的概率都是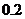 .
.
(1)求这批产品不能出厂的概率(保留三位有效数字);
(2)求直至五项指标全部验完毕,才能确定该批食品是否出厂的概率(保留三位有效数字).
解:(1)这批食品不能出厂的概率是: 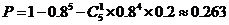 .
(2)五项指标全部检验完毕,这批食品可以出厂的概率是:
.
(2)五项指标全部检验完毕,这批食品可以出厂的概率是:
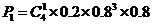 五项指标全部检验完毕,这批食品不能出厂的概率是:
五项指标全部检验完毕,这批食品不能出厂的概率是:
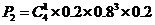 由互斥事件有一个发生的概率加法可知,五项指标全部检验完毕,才能确定这批产品是否出厂的概率是:
由互斥事件有一个发生的概率加法可知,五项指标全部检验完毕,才能确定这批产品是否出厂的概率是: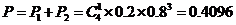 .
.
9.某保险公司新开设了一项保险业务,若在一年内事件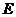 发生,该公司要赔偿
发生,该公司要赔偿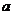 元.设在一年内
元.设在一年内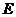 发生的概率为
发生的概率为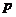 ,为使公司收益的期望值等于
,为使公司收益的期望值等于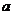 的百分之十,公司应要求顾客交多少保险金?
的百分之十,公司应要求顾客交多少保险金?
解:设保险公司要求顾客交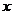 元保险金,若以
元保险金,若以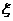 表示公司每年的收益额,则
表示公司每年的收益额,则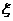 是一个随机变量,其分布列为:
是一个随机变量,其分布列为:
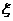
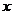
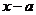
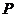
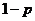
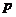
因此,公司每年收益的期望值为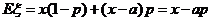 .
为使公司收益的期望值等于
.
为使公司收益的期望值等于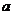 的百分之十,只需
的百分之十,只需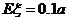 ,即
,即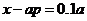 ,
故可得
,
故可得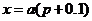 .
即顾客交的保险金为
.
即顾客交的保险金为 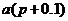 时,可使公司期望获益
时,可使公司期望获益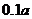 .
.
8.甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为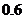 ,被甲或乙解出的概率为
,被甲或乙解出的概率为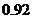 ,(1)求该题被乙独立解出的概率;(2)求解出该题的人数
,(1)求该题被乙独立解出的概率;(2)求解出该题的人数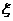 的数学期望和方差
的数学期望和方差
解:(1)记甲、乙分别解出此题的事件记为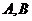 .
.
设甲独立解出此题的概率为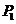 ,乙为
,乙为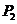 .
.
则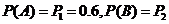
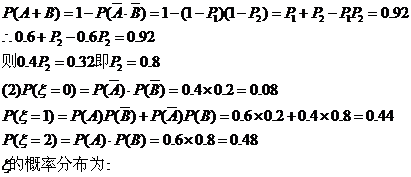
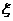
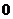
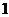
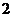
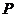
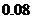
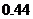
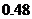
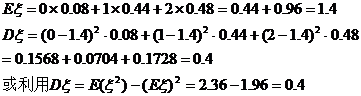
7.要制造一种机器零件,甲机床废品率为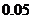 ,而乙机床废品率为
,而乙机床废品率为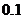 ,而它们
,而它们
的生产是独立的,从它们制造的产品中,分别任意抽取一件,求:
(1)其中至少有一件废品的概率;(2)其中至多有一件废品的概率.
解:设事件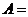 “从甲机床抽得的一件是废品”;
“从甲机床抽得的一件是废品”;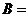 “从乙机床抽得的一件是废品”.
“从乙机床抽得的一件是废品”.
则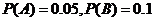
(1)至少有一件废品的概率
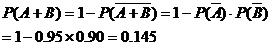
(2)至多有一件废品的概率
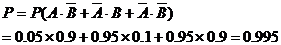
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com